[湖北]2013-2014学年湖北武汉部分学校八年级12月月考数学试卷
在等腰三角形、圆、长方形、正方形、直角三角形中,一定是轴对称图形的有( )个.
| A.1 | B.2 | C.3 | D.4 |
在直角坐标系中,点P(a,2)与点A(-3,m)关于y轴对称,则a、m的值分别为( ).
| A.3,-2 | B.-3,-2 | C.3,2 | D.-3,2 |
如图,在△ABC中,∠A=72°,AB=AC,BD平分∠ABC,且BD=BE,点D、E分别在AC、BC上,则∠DEB=( ).
A.76° B.75.5° C.76.5° D.75°
如图,已知AB∥CD,AB=CD,添加条件( )能使△ABE≌△CDF.
| A.AF=EF | B.∠B=∠C | C.EF=CE | D.AF=CE |
如图,△ABC中,∠ACB=90°,AC=4,BC=3,AB=5,CH⊥AB于H,则CH的长为( ).
| A.2.4 | B.3 | C.2.2 | D.3.2 |
如图,已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在 处,
处, 分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为( ).
分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为( ).
A.45°B.50°C.55°D.60°
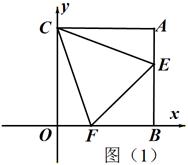
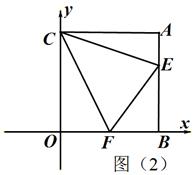
如图,正方形CEFH的边长为m,点D在射线CH上移动,以CD为边作正方形CDAB,连接AE、AH、HE,在D点移动的过程中,三角形AHE的面积( ).
| A.无法确定 | B. m2 m2 |
C. m2 m2 |
D. m2 m2 |
如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则图中的等腰三角形共有( )个.
如图,△ABC内有一点D,且DA=DB=DC,若∠ACD=30°,∠BCD=40°,则∠ADB的大小是( ).
如图,在直角坐标系中,已知点A(-3,4)、B(5,4),在x轴上找一点P,使PA+PB最小,则P点坐标为( ).
如图,点D、E分别在线段AB、AC上,已知AD=AE,∠B=∠C,H为线段BE、CD的交点,求证:BH=CH.
如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(2,2)、B(-1,-2)、C(-1,1).
(1)(画图与写坐标各3分)画出与△ABC关于y轴对称的△A1B1C1,A、B、C的对称点分别为A1、B1、C1,则点A1、B1、C1的坐标分别为( )、( )、( ).
(2)画出B点关于C点的对称点B2(保留作图痕迹),并求出其坐标.
△ABC的周长为22cm,AB边比AC边长2cm,BC边是AC边的一半,求△ABC三边的长.
已知二次三项式mx2-nx+1与一次二项式2x-3的积不含x2项,也不含x项,求系数m、n的值.
△ABC中,射线AD平分∠BAC,AD交边BC于E点.
(1)如图1,若AB=AC,∠BAC=90°,则 ( )
( ) ;
;
(2)如图2,若AB≠AC,则(1)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,若AB>AC,∠BAC=∠BDC=90°,∠ABD为锐角,DH⊥AB于H,则线段AB、AC、BH之间的数量关系是( ),并证明.
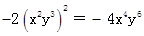
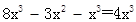
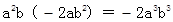
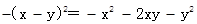











 能用完全平方式分解因式,则m的值为( ).
能用完全平方式分解因式,则m的值为( ).




 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号