[黑龙江]2014届黑龙江省大庆市高三9月第一次教学质量检测理科数学试卷
已知集合 ,
, ,则
,则 =( )
=( )
| A.{2,4,6} | B.{1,3,5} | C.{3,5,6} | D.U |
函数 的零点一定位于区间( )
的零点一定位于区间( )
| A.(1, 2) | B.(2, 3) | C.(3, 4) | D.(4, 5) |
要得到函数 的图象,只要将函数y=sin2x的图象( )
的图象,只要将函数y=sin2x的图象( )
A.向左平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向右平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
如果执行下面的程序框图,那么输出的s=( )
| A.121 | B.132 | C.1320 | D.11880 |
如图,网格纸上小正方形的边长为1,粗线画的是某几何体的视图,则其体积为( )
A.12+ |
B.24+ |
C.32+ |
D.24+ |
下列命题中,真命题是( )
A.直线m、n都平行于平面 ,则m∥n ,则m∥n |
B.设 是真二面角,若直线 是真二面角,若直线 ,则 ,则 |
C.设m、n是异面直线,若m∥平面 ,则n与 ,则n与 相交 相交 |
D.若直线m、n在平面 内的射影依次是一个点和一条直线,且 内的射影依次是一个点和一条直线,且 ,则 ,则 或 或 |
已知实数x,y满足 ,则目标函数z=x-y的最小值为( )
,则目标函数z=x-y的最小值为( )
| A.-2 | B.5 | C.6 | D.7 |
已知A,B是双曲线 的两个顶点,P为双曲线上(除顶点外)的一点,若直线PA,PB的斜率乘积为
的两个顶点,P为双曲线上(除顶点外)的一点,若直线PA,PB的斜率乘积为 ,则双曲线的离心率e=( )
,则双曲线的离心率e=( )
A. |
B. |
C. |
D. |
已知函数f(x)的定义域为R,对任意 ,有
,有 ,且
,且 ,则f(x)<3x+6的解集为( )
,则f(x)<3x+6的解集为( )
| A.(-1, 1) | B.(-1,+ ) ) |
C.(- ,-1) ,-1) |
D.(- ,+ ,+ ) ) |
抛物线y2=4x的焦点为F,点A,B在抛物线上,且 ,弦AB中点M在准线l上的射影为
,弦AB中点M在准线l上的射影为 ,则
,则 的最大值为( )
的最大值为( )
A. |
B. |
C. |
D. |
从8名女生,4名男生中,选出2名女生,1名男生组成课外小组,则不同的选取方案种数为_______________(用数字作答).
已知在等差数列{ }中,
}中, =3,前7项和
=3,前7项和 =28.
=28.
(I)求数列{ }的公差d;
}的公差d;
(II)若数列{ }为等比数列,且
}为等比数列,且 ,
, 求数列
求数列 的前n项和
的前n项和
 .
.
已知角A,B,C是△ABC三边a,b,c所对的角, ,
, ,
, ,且
,且 .
.
(I)若△ABC的面积S= ,求b+c的值;
,求b+c的值;
(II)求b+c的取值范围.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= ,AD=1.
,AD=1.
(I)求证:CD⊥平面PAC;
(II)求二面角A-PD-C的余弦值.
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |
[70,76) |
[76,82) |
[82,88) |
[88,94) |
[94,100] |
| 元件A |
8 |
12 |
40 |
32 |
8 |
| 元件B |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计元件A,元件B为正品的概率;
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
已知函数 .
.
(I)求f(x)的单调区间及极值;
(II)若关于x的不等式 恒成立,求实数a的集合.
恒成立,求实数a的集合.
 是两夹角为120°的单位向量,
是两夹角为120°的单位向量, ,则
,则 等于( )
等于( )

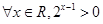
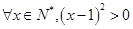

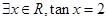
 的共轭复数为_____________.
的共轭复数为_____________. 的倾斜角最小的切线,则l的方程为____________.
的倾斜角最小的切线,则l的方程为____________. ,则
,则 ____________.
____________. )在椭圆C上.
)在椭圆C上.
 :
: 与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且
与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且 ,
, ,四边形
,四边形 面积S的求最大值.
面积S的求最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号