广东省东莞市五校高三第一次联考文科数学卷
为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( )
A.向左平移 个单位 个单位 |
B.向左平移 个单位 个单位 |
C.向右平移 个单位 个单位 |
D.向右平移 个单位 个单位 |
来源:2011届广东省东莞五校高三第一次联考文科数学卷
“ ”是“直线
”是“直线 和直线
和直线 互相垂直”的( )
互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2011届广东省东莞五校高三第一次联考文科数学卷
.设抛物线 的焦点为
的焦点为 ,准线为
,准线为 ,
, 为抛物线上一点,
为抛物线上一点, 为垂足. 如果直线
为垂足. 如果直线 的斜率为
的斜率为 ,那么
,那么 ( )
( )
A. |
B.8 | C. |
D.16 |
来源:2011届广东省东莞五校高三第一次联考文科数学卷
某几何体的一条棱长为 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为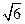 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为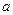 和
和 的线段,则
的线段,则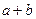 的最大值为( )
的最大值为( )
A.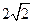 |
B.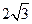 |
C.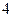 |
D. W$ W$ |
来源:2011届广东省东莞五校高三第一次联考文科数学卷
如图,椭圆的中心在原点, 为椭圆的左焦点,
为椭圆的左焦点,  为椭圆的一个顶点,过点
为椭圆的一个顶点,过点 作与
作与 垂直的直线
垂直的直线 交
交 轴于
轴于 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长 和短半轴长
和短半轴长 是关于
是关于 的方程
的方程 (其中
(其中 为半焦距)的两个根.
为半焦距)的两个根.
(1)求椭圆的离心率;
(2)经过 、
、 、
、 三点的圆与直线
三点的圆与直线 相切,试求椭圆的方程.
相切,试求椭圆的方程.
来源:2011届广东省东莞五校高三第一次联考文科数学卷
 ,
, 的子集中,含有元素
的子集中,含有元素 的子集共有 ( )
的子集共有 ( ) ,则使得
,则使得 为奇函数,且在
为奇函数,且在 上单调递减的
上单调递减的 的个数是( )
的个数是( )  ,则
,则 ( )
( )


 、
、 和平面
和平面 、
、 ,下列四个命题中,正确的是( )
,下列四个命题中,正确的是( ) ,则
,则
 ,则
,则
 ,则
,则
 ,则
,则
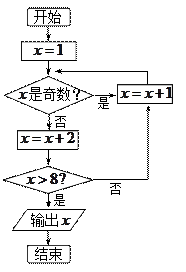
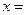 ( )
( )
 和
和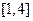 内任取一个实数,
内任取一个实数, 和
和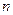 ,则
,则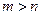 的概率是( )
的概率是( )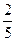
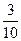
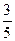

 的共轭复数为 ;
的共轭复数为 ; 的两根中,一根在
的两根中,一根在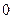 和
和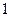 之间,另一根在
之间,另一根在 之间,则实数
之间,则实数 的取值范围是 ;
的取值范围是 ;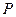 为曲线
为曲线 上一点,曲线
上一点,曲线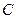 在点
在点 ,则点
,则点 的圆心,且垂直于极轴的直线的极坐标方程为
的圆心,且垂直于极轴的直线的极坐标方程为  是圆
是圆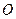 的内接四边形,延长
的内接四边形,延长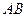 和
和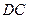 相交于点
相交于点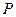 ,若
,若 ,则
,则 的值为 .
的值为 .
 ,且
,且 ,设
,设 函数
函数 在
在 上单调递减;
上单调递减; 函数
函数 有两个不同零点,如果
有两个不同零点,如果 和
和 有且只有一个正确,求
有且只有一个正确,求 的取值范围.
的取值范围. 的面积是
的面积是 ,内角
,内角 所对边长分别为
所对边长分别为
 (1)求
(1)求 ; (2)若
; (2)若 , 求
, 求 的值
的值 为矩形,
为矩形, 、
、 分别是线段
分别是线段 、
、 的中点,
的中点, 平面
平面 (1)求证:
(1)求证: ;
; 在
在 上,且
上,且 平面
平面 ,试确定点
,试确定点 (
( 为实常数).
为实常数). 时,求
时,求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求
 时, 证明: 不等式
时, 证明: 不等式 恒成立;
恒成立;  满足
满足 ,证明数列
,证明数列 是等比数列,并求出数列
是等比数列,并求出数列 ,证明:
,证明: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号