[山西]2013年初中毕业升学考试(山西卷)数学
某班实行每周量化考核制,学期末对考核成绩进行统计,结果显示甲、乙两组的平均成绩相同,方差分别是S2甲=36,S2乙=30,则两组成绩的稳定性:
| A.甲组比乙组的成绩稳定 | B.乙组比甲组的成绩稳定 |
| C.甲、乙两组的成绩一样稳定 | D.无法确定 |
下表是我省11个地市5月份某日最高气温(℃)的统计结果:
| 太原 |
大同 |
朔州 |
忻州 |
阳泉 |
晋中 |
吕梁 |
长治 |
晋城 |
临汾 |
运城 |
| 27 |
27 |
28 |
28 |
27 |
29 |
28 |
28 |
30 |
30 |
31 |
该日最高气温的众数和中位数分别是
A.27℃,28℃ B.28℃,28℃ C.27℃,27℃ D.28℃,29℃
王先生到银行存了一笔三年期的定期存款,年利率是4.25%,若到期后取出得到本息和(本金+利息)33852元。设王先生存入的本金为x元,则下面所列方程正确的是
| A.x+3×4.25%x=33825 | B.x+4.25%x=33825 |
| C.3×4.25%x=33825 | D.3(x+4.25%x)="33825" |
如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则BC两地之间的距离为
A.100 m m |
B.50 m m |
C.50 m m |
D. m m |
起重机将质量为6.5t的货物沿竖直方向提升了2m,则起重机提升货物所做的功用科学记数法表示为(g=10N/kg)
| A.1.3×106J | B.13×105J | C.13×104J | D.1.3×105J |
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是
A. |
B. |
C. |
D. |
四川雅安发生地震后,某校九(1)班学生开展献爱心活动,积极向灾区捐款。如图是该班同学捐款的条形统计图,写出一条你从图中所获得的信息: . 
如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线 经过点C交x轴于点E,双曲线
经过点C交x轴于点E,双曲线 经过点D,则k的值为 .
经过点D,则k的值为 .
如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 .
如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7m,则DE的长为 m. 
(1)计算: .
.
(2)下面是小明化简分式的过程,请仔细阅读,并解答所提出的问题。 ………………………第一步
………………………第一步 …………………………………………………………第二步
…………………………………………………………第二步 ……………………………………………………………第三步
……………………………………………………………第三步 ………………………………………………………………………第四步
………………………………………………………………………第四步 小明的解法从第 步开始出现错误,正确的化简结果是 。
小明的解法从第 步开始出现错误,正确的化简结果是 。
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点。
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作∠DAC的平分线AM。②连接BE并延长交AM于点F。
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由。
小勇收集了我省四张著名的旅游景点图片(大小、形状及背面完全相同):太原以南的壶口瀑布和平遥古城,太原以北的云岗石窟和五台山。他与爸爸玩游戏:把这四张图片背面朝上洗匀后,随机抽取一张(不放回),再抽取一张,若抽到两个景点都在太原以南或都在太原以北,则爸爸同意带他到这两个景点旅游,否则,只能去一个景点旅游。请你用列表或画树状图的方法求小勇能去两个景点旅游的概率(四张图片分别用(H,P,Y,W表示)。
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q。
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由。
(2)若cosB= ,BP=6,AP=1,求QC的长。
,BP=6,AP=1,求QC的长。
某校实行学案式教学,需印制若干份数学学案。印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要。两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的函数关系式是 .
乙种收费方式的函数关系式是 .
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算。
数学活动——求重叠部分的面积。
问题情境:数学活动课上,老师出示了一个问题:
如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,DE经过点C,DF交AC于点G。
求重叠部分(△DCG)的面积。
(1)独立思考:请解答老师提出的问题。
(2)合作交流:“希望”小组受此问题的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图(2),你能求出重叠部分(△DGH)的面积吗?请写出解答过程。
(3)提出问题:老师要求各小组向“希望”小组学习,将△DEF绕点D旋转,再提出一个求重叠部分面积的问题。“爱心”小组提出的问题是:如图(3),将△DEF绕点D旋转,DE,DF分别交AC于点M,N,使DM=MN,求重叠部分(△DMN)的面积。
任务:①请解决“爱心”小组所提出的问题,直接写出△DMN的面积是 .
②请你仿照以上两个小组,大胆提出一个符合老师要求的问题,并在图中画出图形,标明字母,不必解答(注:也可在图(1)的基础上按顺时针方向旋转)。
综合与探究:如图,抛物线 与x轴交于A,B两点(点B在点A的右侧)与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q。
与x轴交于A,B两点(点B在点A的右侧)与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q。
(1)求点A,B,C的坐标。
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N。试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由。
(3)当点P在线段EB上运动时,是否存在点 Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由。
 的结果是
的结果是 的解集在数轴上表示为
的解集在数轴上表示为












 时,去分母后变形为
时,去分母后变形为




 .
.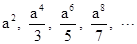 则第n个式子是 .
则第n个式子是 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号