[山东]2013年初中毕业升学考试(山东德州卷)数学
民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也不是轴对称图形的是
A. |
B. |
C. |
D. |
森林是地球之肺,每年能为人类提供大约28.3亿吨的有机物.28.3亿吨用科学记数法表示为
| A.28.3×107 | B.2.83×108 | C.0.283×1010 | D.2.83×109 |
如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为
| A.68° | B.32° | C.22° | D.16° |
甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是
| A.甲、乙两人的速度相同 | B.甲先到达终点 |
| C.乙用的时间短 | D.乙比甲跑的路程多 |
下列命题中,真命题是
| A.对角线相等的四边形是等腰梯形 |
| B.对角线互相垂直平分的四边形是正方形 |
| C.对角线互相垂直的四边形是菱形 |
| D.四个角相等的四边形是矩形 |
一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于 n2,则算过关;否则不算过关,则能过第二关的概率是
n2,则算过关;否则不算过关,则能过第二关的概率是
A. |
B. |
C. |
D. |
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为
A. |
B. |
C. |
D. |
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为
| A.1 | B.2 | C.3 | D.4 |
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为
| A.(1,4) | B.(5,0) | C.(6,4) | D.(8,3) |
甲乙两种水稻试验品中连续5年的平均单位面积产量如下(单位:吨/公顷)
| 品种 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
品种 |
| 甲 |
9.8 |
9.9 |
10.1 |
10 |
10.2 |
甲 |
| 乙 |
9.4 |
10.3 |
10.8 |
9.7 |
9.8 |
乙 |
经计算,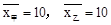 ,试根据这组数据估计 中水稻品种的产量比较稳定.
,试根据这组数据估计 中水稻品种的产量比较稳定.
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD= .
.
其中正确的序号是 (把你认为正确的都填上).
某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
| 分组 |
划记 |
频数 |
| 2.0<x≤3.5 |
正正 |
11 |
| 3.5<x≤5.0 |
 |
19 |
| 5.0<x≤6.5 |
|
|
| 6.5<x≤8.0 |
|
|
| 8.0<x≤9.5 |
 |
2 |
| 合计 |
|
50 |

(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
(1)求AD的长;
(2)BC是⊙O的切线吗?若是,给出证明;若不是,说明理由.
某地计划用120﹣180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石比原计划多5000米3,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1.
| 1 |
2 |
3 |
﹣7 |
| ﹣2 |
﹣1 |
0 |
1 |
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
| a |
a2﹣1 |
﹣a |
﹣a2 |
| 2﹣a |
1﹣a2 |
a﹣2 |
a2 |
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹);
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.









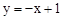
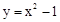
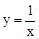
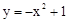
 的值是 .
的值是 .
 与y=x﹣2图象交点的横坐标分别为a,b,则
与y=x﹣2图象交点的横坐标分别为a,b,则 的值为 .
的值为 . ,其中
,其中 .
. 经过点A、B、C.
经过点A、B、C.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号