河南省扶沟县初一下学期直方图检测题
一条长度为10cm的线段,当它绕线段的 旋转一周时,线段“扫描”过的圆面积最大,此时最大面积为 ;当它绕线段的 旋转一周时,线段“扫描”经过的圆面积最小,此时最小面积为
如图1, 中
中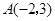 ,
,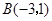 ,
,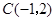 .
.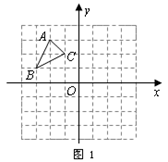
(1)将 向右平移
向右平移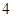 个单位长度,画出平移后的
个单位长度,画出平移后的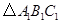 ;
;
(2)画出 关于
关于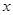 轴对称的
轴对称的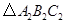 ;
;
(3)将 绕原点
绕原点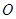 旋转
旋转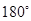 ,画出旋转后的
,画出旋转后的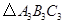 ;
;
(4)在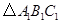 ,
, ,
, 中,
中, ______与
______与 ______成轴对称,对称轴是______;
______成轴对称,对称轴是______; ______与
______与 ______成中心对称,对称中心的坐标是____
______成中心对称,对称中心的坐标是____
要对一块长60米、宽40米的矩形荒地 进行绿化和硬化.
进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形 面积的
面积的 ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为 和
和 ,且
,且 到
到 的距离与
的距离与 到
到 的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
已知 用含的
用含的 代数式表示
代数式表示 .甲、乙两位同学跑上讲台,板书了下面两种解法:
.甲、乙两位同学跑上讲台,板书了下面两种解法:
同学甲解: 
同学乙解:
因为 ,
,  .
.
老师看罢,提出下面的问题:
(1)两位同学的解法都正确吗?为什么?
(2)请你再给出一种不同于甲、乙二人的解法
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量 达到100辆.
达到100辆.
(1)若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少 辆?
辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两 种车位各多少个?试写出所有可能的方案
种车位各多少个?试写出所有可能的方案
如图,在直角坐 标系中,已知点P0的坐标
标系中,已知点P0的坐标 为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此
为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此 下去,得到线段OP3,OP4,…,OPn(n为正整数)
下去,得到线段OP3,OP4,…,OPn(n为正整数)
(1)求点P6的坐标;
(2)求△P5OP6的面积;
(3)我们规定:把点Pn(xn,yn)(n=0,1,2,3…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Pn的“绝对坐标”.根据图中点Pn的分布规律,请你猜想点Pn的“绝对坐标”,并写出来
在以下现象中:①温度计中液面上升或下降,②用打气筒打气时活塞的移动,③钟摆的摆动,④传送带带着瓶装饮料的移动。其中平移的有( )
| A.①②④ | B.①③ | C.②③ | D.②④ |
在平移过程中,对应线段( )
| A.互相平行且相等 | B.互相垂直且相等 |
| C.互相平行(或在同一条直线上)且相等 | D.相交且相等 |
绘制频数分布直方图时,各个小长方形的高等于相应各组的( )
(A)组距 (B)平均值 (C)频数 (D)百分比
在频率分布直方图中,各个小长方形的面积表示( )
| A.落在相应各组的数据的频数 | B.相应各组的频率 |
| C.该样本所分成的组数 | D.该样本的样本容量 |
某班共有学生40人,在一次数学测试中共有20人的成绩在80分以上,这次测试中80分以上的成绩出现的频数是( )
| A.20 | B.0.5 | C. 40 | D. 80 |
在100个数据中用适当的方法抽取50个作为样本进行统计,频率分布表中,54.5~57.5这一组的频率为0.12,则估计总体数据落在54.5~57.5之间的约有( )
| A.6个 | B.12个 | C.60个 | D.120个 |
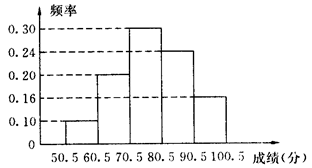
某校为了了解九年级学生的体能情况,随机抽查了其中30名学生,测试了他们做1min仰卧起坐的次数,并制成了如图所示的频数分布直方图,根据图示计算仰卧起坐次数在25~30次的频率是( ).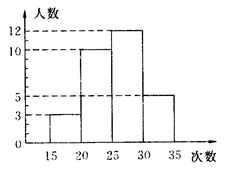
| A.0.1 | B.0.2 | C.0.3 | D.0.4 |
一个样本含有20个数据:35,31,33,35,37,39,35,38,40,39,36,34,35,37,36,32,34,35,36,34.
在列频数分布表时,如果组距为2,那么应分成___ 组,32.5~34.5这组的频数为___
对某班同学的身高进行统计(单位:厘米),频数分布表中165.5~170.5这一组学生人数是12,频率是0.25,则该班共有____名学生
下表是某班学生在一次身高测量中得到的统计结果:
请回答:
(1)这个班总人数是 人;身高 、 的人数最多,分别有 人、 人.
(2)身高最高、最低的分别是 m、 m,他们分别有 人、 人;身高最高的与最低的相差 m.
如果将频率分布直方图中各相邻矩形的上底边的中点顺次连接起来,得到的折线,我们称之为这组数据的_____________
某工厂有3条流水线生产同一种产品.在每条流水线上,每生产若干产品就要抽取1件产品进行检验.某日共检验150件产品.已知第1、2、3三条流水线上所生产的产品数之比为2:3:5,则这一天在第2条流水线上共检验了_______件产品
如图是某校七年一班全班同学1min心跳次数频数直方图,那么,心跳次数在___之间的学生最多,占统计人数的____%.(精确到1%)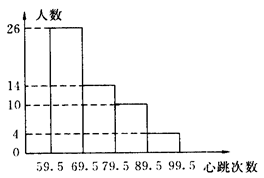
在某次学生考试的成绩中随机抽取若干学生的成绩,分组与各组的频数如下:[40, 50),4;[50,60),1;[60,70),10;[70,80),11;[80,90),18;[90,100),6,估计本次考试的及格率为______
已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图
如图,从参加环保知识竞赛的 学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:
学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下: 观察图形,回答下列问题:
观察图形,回答下列问题: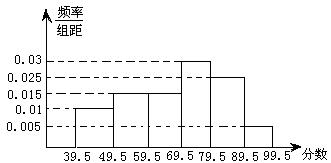
(1)79.5---89.5这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格)
为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 |
频数 |
频率 |
| 145.5~149.5 |
1 |
0.02 |
| 149.5~153.5 |
4 |
0.08 |
| 153.5~157.5 |
20 |
0.40 |
| 157.5~161.5 |
15 |
0.30 |
| 161.5~165.5 |
8 |
0.16 |
| 165.5~169.5 |
m |
n |
| 合 计 |
M |
N |
(1)求出表中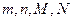 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?
七年级(1)班40个学生某次数学测验成绩如下(单位:分):
63 84 91 53 69 81 61 69 91 78
75 81 80 67 76 81 79 94 61  69
69
89 70 70 87 81 86 90 88 85 67
67
71 82 87 75 87 95 53 65 74 77
数学老师按10分的组距分段,算出每个分数段学生成绩出现的频数,填入频数分布表.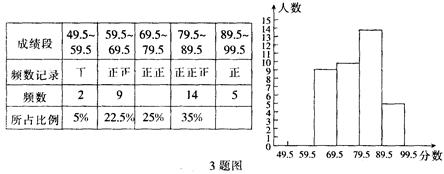
(1)请把频数分布表及频数分布直方图补充完整;
(2)请你帮老师统计一下这次数学考试的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀);
(3)请说明哪个分数段的学生最多?哪个分数段的学生最少?
(4)绘制频数折线图.
2 011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
| 分组 |
频数 |
频率 |
|
| 一组 |
0 <5 <5 |
0 |
0 |
| 二组 |
5 <10 <10 |
10 |
0.10 |
| 三组 |
10 <15 <15 |
10 |
|
| 四组 |
15 <20 <20 |
|
0.50 |
| 五组 |
20 <25 <25 |
30 |
0.30 |
| 合计 |
100 |
1.00 |
(1)在表中填写缺失的数据;
(2)画出频数分布直方图;
(3)求购票时间的平均数
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么 决策一下至少要增加几个窗口?
 ,根据这个规则,方程(x+2) *5=0的解为______
,根据这个规则,方程(x+2) *5=0的解为______ =11;同样,因为1112=12321,所以
=11;同样,因为1112=12321,所以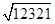 =111;…由此猜想
=111;…由此猜想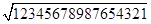 =_
=_


 、
、 为实数,且满足
为实数,且满足
 的值
的值 平移到
平移到 ,则图中平行相等的线段有_____对( )
,则图中平行相等的线段有_____对( )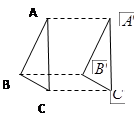
 平移后得到
平移后得到 ,则和
,则和 对应的线段是( )
对应的线段是( )



 经过平移后得到
经过平移后得到 ,则
,则 的对应角和
的对应角和 的对应边分别是( )
的对应边分别是( )
 、
、
 、
、
 ,
, 是沿
是沿 方向平移后的图形,试判断
方向平移后的图形,试判断 与
与 的面积关系是___________
的面积关系是___________
 的汽车大约有_____辆
的汽车大约有_____辆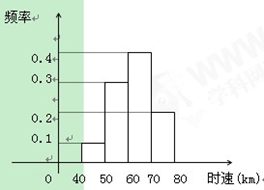
 粤公网安备 44130202000953号
粤公网安备 44130202000953号