[湖北]2012-2013学年湖北省武汉市青山区七年级第一学期期末测试数学试卷
若火箭发射点火后3秒记为+3秒,那么火箭发射点火前10秒应记为( )
| A.-10秒 | B.+10秒 | C.-3秒 | D.+3秒 |
某市在一次扶贫助残活动中,捐款约3180000元,请将3180000元用科学记数法表示为( )
| A.0.318×106元 | B.3.18×106元 | C.31.8×106元 | D.318×106元 |
下列各组式子中,属于同类项的是( )
A. ab与 ab与 b b |
B.ab与ac | C. xy与-2yx xy与-2yx |
D.a与b |
已知关于x的方程2x+a-9=0的解是x=2,则a的值为( )
| A.2 | B.3 | C.4 | D.5 |
如图,如果射线OA表示在阳光下你的身影的方向,那么你的身影的方向是( ) 
| A.北偏东60° | B.南偏西60° | C.北偏东30° | D.南偏西30° |
如图,已知点C是线段AB的中点,且AC=3,则AB的长为( )
A. |
B.3 | C.6 | D.12 |
下列运算正确的是( )
| A.m-2(n-7) =m-2n-14 | B.- = = |
| C.2x+3x=5x2 | D.x-y+z="x-(y-z)" |
如图所示的图案是由小三角形按一定规律排列而成,依此规律,第n个图中小三角形的个数为2011个,则n的相反数为( )
| A.670 | B.671 | C.-670 | D.-671 |
武汉市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上银杏树,要求路的两端各栽一棵,并且每两棵树的问隔相等.如果每隔5米栽l棵,则树苗缺21棵;如果每隔6米栽l棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
| A.5(x+21-1)=6(x-l) | B.5(x+21)=6(x-l) |
| C.5(x+21-1)=6x | D.5(x+21)=6x |
如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,则以下结论:①∠AOE=∠DOE;②∠AOD+∠COB=180°;③∠COB-∠AOD=90°;④∠COE+∠BOF=180°.其中正确结论的个数有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
笔记本的单价是m元,圆珠笔的单价是n元,小明买了2本笔记本,3支圆珠笔;小军买了3本笔记本,5支圆珠笔,则小明和小军共花了_____元钱.
如图,已知D、E是线段BC上的一点,连结AB. AD. AE. AC.下列说法:①∠DAE可记作∠1;②∠2可记作∠E;③图中有且只有2个角可以用一个大写字母表示;④图中共有10条线段;⑤图中共有10个小于平角的角.其中正确的是______;(填序号)
若a、b互为相反数,c、d互为负倒数,p的绝对值等于2,则关于x的方程(a+b)x+3cdx-p2=O的解为________;
将一副三角尺按照如图的位置摆放,使得三角尺ACB的直角顶点C在三角尺DEF的直角边EF上.
(1)求∠ 十∠
十∠ 的度数;
的度数;
(2)若∠ =32°,试问∠
=32°,试问∠ 的补角为多少度?
的补角为多少度?
如图,点A、B.、C在同一条直线上,D为AC的中点,且AB=6cm,BC=2cm.
(1)试求AD的长;
(2)求AD:BD的值。
(如图,已知∠AOB=ll0°,∠AOC=m∠AOD,∠COE=n∠BOC,且3(m-2)+4=m+2,单项式 的系数为n.
的系数为n.
(1)求4(m-n) 2-(m-n) 2-5的值;
(2)当∠COD:∠COE=3:2时,试求∠COD的度数.
平价商场经销甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元.
(1)甲种商品每件进价为______元,每件乙种商品利润率为_____;
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2100元,求购进甲种商品多少件?
(3)在“元旦”期间,该商场只对甲乙两种商品进行如下的优惠促销活动:
| 打折前一次性购物总金额 |
优惠措施 |
| 不超过380元 |
不优惠 |
| 超过380元,但不超过500元 |
售价打九折 |
| 超过500元 |
售价打八折 |
按上述优惠条件,若小聪第一天只购买乙种商品,实际付款360元,第二天只购买甲种商品实际付款432元,求小聪这两天在该商场购买甲、乙两种商品一共多少件?
如图1,已知点A、C、F、E、B为直线l上的点,且AB=12,CE=6,F为AE的中点.
(1)如图1,若CF=2,则BE=______,若CF=m,BE与CF的数量关系是______;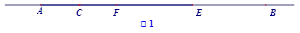
(2)当点E沿直线l向左运动至图2的位置时,(1)中BE与CF的数量关系是否仍然成立?请说明理由.
(3)如图3,在(2)的条件下,在线段BE上,是否存在点D,使得BD=7,且DF=3DE?若存在,请求出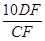 值;若不存在,请说明理由.
值;若不存在,请说明理由.
如图l,已知∠AOC=m°,∠BOC=n°且m、n满足等式|3m-420|+(2n-40)2=0,射线OP从OB处绕点0以4度/秒的速度逆时针旋转.
(1)试求∠AOB的度数;
(2)如图l,当射线OP从OB处绕点O开始逆时针旋转,同时射线OQ从OA处以l度/秒的速度绕点0顺时针旋转,当他们旋转多少秒时,使得∠POQ=10°?
(3)如图2,若射线OD为∠AOC的平分线,当射线OP从OB处绕点O开始逆时针旋转,同时射线OT从射线OD处以x度/秒的速度绕点O顺时针旋转,使得这两条射线重合于射线OE处(OE在∠DOC的内部)时,且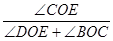 =
= ,试求x.
,试求x.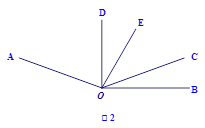


 =2+
=2+

 粤公网安备 44130202000953号
粤公网安备 44130202000953号