[重庆]2013届重庆市高三九校联合诊断考试理科数学试卷
已知 ,那么角
,那么角 是( )
是( )
| A.第一或第二象限角 | B.第二或第三象限角 |
| C.第三或第四象限角 | D.第一或第四象限角 |
来源:2013届重庆市高三九校联合诊断考试理科数学试题
下图给出4个幂函数的图象,则图象与函数的大致对应是( )
A.① ② ② ③ ③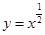 ④ ④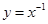 |
B.① ② ② ③ ③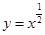 ④ ④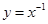 |
C.① ② ② ③ ③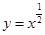 ④ ④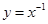 |
D.① ② ②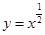 ③ ③ ④ ④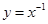 |
来源:2013届重庆市高三九校联合诊断考试理科数学试题
已知直线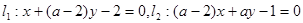 ,则“
,则“ ”是 “
”是 “ 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
来源:2013届重庆市高三九校联合诊断考试理科数学试题
设双曲线  的右焦点为
的右焦点为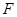 ,右准线
,右准线  与两条渐近线交于
与两条渐近线交于 两点,如果
两点,如果 是等边三角形,则双曲线的离心率
是等边三角形,则双曲线的离心率 的值为( )
的值为( )
A. |
B. |
C. |
D. |
来源:2013届重庆市高三九校联合诊断考试理科数学试题
规定记号“ ”表示一种运算,即:
”表示一种运算,即: ,设函数
,设函数 。且关于
。且关于 的方程为
的方程为 恰有四个互不相等的实数根
恰有四个互不相等的实数根 ,则
,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
来源:2013届重庆市高三九校联合诊断考试理科数学试题
已知函数 的定义域为
的定义域为 部分对应值如下表,
部分对应值如下表, 为
为 的导函数,函数
的导函数,函数 的图象如图所示:
的图象如图所示:
 |
-2 |
0 |
4 |
 |
1 |
-1 |
1 |

若两正数 满足
满足 ,则
,则 的取值范围是 .
的取值范围是 .
来源:2013届重庆市高三九校联合诊断考试理科数学试题
已知 与两平行直线
与两平行直线 都相切,且圆心
都相切,且圆心 在直线
在直线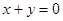 上,
上,
(Ⅰ)求 的方程;
的方程;
(Ⅱ)斜率为2的直线 与
与 相交于
相交于 两点,
两点, 为坐标原点且满足
为坐标原点且满足 ,求直线
,求直线 的方程。
的方程。
来源:2013届重庆市高三九校联合诊断考试理科数学试题
如图,在平面直坐标系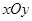 中,已知椭圆
中,已知椭圆 ,经过点
,经过点 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆 与直线
与直线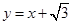 有且只有一个交点。
有且只有一个交点。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设不经过原点的直线 与椭圆
与椭圆 相交与A,B两点,第一象限内的点
相交与A,B两点,第一象限内的点 在椭圆上,直线
在椭圆上,直线 平分线段
平分线段 ,求:当
,求:当 的面积取得最大值时直线
的面积取得最大值时直线 的方程。
的方程。
来源:2013届重庆市高三九校联合诊断考试理科数学试题
 满足
满足 ,则复数
,则复数

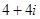

 为单位向量,
为单位向量, ,且
,且 ,则
,则 与
与


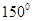
 下列不等式中正确的是( )
下列不等式中正确的是( )




 是
是 的充要条件
的充要条件
 的否定是真命题。
的否定是真命题。 满足约束条件
满足约束条件 则
则 的最小值为( )
的最小值为( )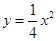 ,则它的焦点坐标为 .
,则它的焦点坐标为 . ,则
,则 .
. 的图象与
的图象与 轴所围成的封闭图形的面积为 .
轴所围成的封闭图形的面积为 . 满足
满足 ,
, ,则数列
,则数列 .
.
 的最小正周期;
的最小正周期; ,求函数
,求函数 中,内角
中,内角 对边的边长分别是
对边的边长分别是 , 且
, 且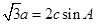

 ,
,  ,求ΔABC的面积
,求ΔABC的面积
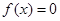 有三个不同的实根.
有三个不同的实根.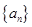 的前
的前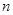 项和为
项和为 ,满足
,满足 ,且
,且 。
。 的值;
的值; 的前
的前 ,且
,且 ,证明:对一切正整数
,证明:对一切正整数
 粤公网安备 44130202000953号
粤公网安备 44130202000953号