[江苏]2012届江苏扬中市九年级下学期期中考试数学试卷
某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10, 7,9,则这五次射击的平均数是 ▲ 环,方差是 ▲ 环 .
.
如图,△ABC中,∠ACB=900,AC=6,BC=8,D是AB的中点,CE⊥AB于E,则CD= ▲ ,CE= ▲ . 
下列图中有大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n幅图中共有 ▲ 个.
如图,点A在反比例函数 的图像上,点B在反比例函数
的图像上,点B在反比例函数 的图像上,且∠AOB=90°,则tan∠OAB的值为 ▲ .
的图像上,且∠AOB=90°,则tan∠OAB的值为 ▲ .
根据流程右边图中的程序,当输出数值y为1时,输入数值x为( ▲)
| A.-8 | B.8 | C.-8或8 | D.不存在 |
实践应用(本小题满分6分)
国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.2012年,为了了解我市毕业班学生体育活动情况,随机对我市240名毕业班学生进行调查,调查内容为:
以下是根据所得的数据制成的统计图的一部分.
问题:根据以上信息,解答下列问题:
(1)每天在校锻炼时间超过1小时的人数是 ▲ ;
(2)请将条形图补充完整;
(3)2011年我市初中毕业生约为8.4万人,请你估计今年全市初中毕业生中每天锻炼时间低于0.5小时的学生约有多少万人?
实践应用(本小题满分6分)
有两个可以自由转动的均匀转盘A,B都被分成了3等分,并在每一份内均标有数字,如图所示,规则如下:
①分别转动转盘A,B;②两个转盘停止后观察两个指针所指份内的数字(若指针停在等分线上,那么重转一次,直到指针指向某一份内为止).
(1)请用树状图或列表法列出所有可能的结果;
(2)王磊和张浩想用这两个转盘做游戏,他们规定:若“两个指针所指的数字都是方程 的解”时,王磊得1分;若“两个指针所指的数字都不是方程
的解”时,王磊得1分;若“两个指针所指的数字都不是方程 的解”时,张浩得3分,这个游戏公平吗?为什么?
的解”时,张浩得3分,这个游戏公平吗?为什么?
推理证明(本小题满分6分)
如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点, ÐDOC=2ÐACD=90°.

(1)求证:直线AC是圆O的切线;
(2)如果ÐACB=75°,圆O的半径为2,求BD的长.
实践应用(本小题满分6分)
江苏省第八届园博会于2013年在我市举行,宣传部门在一幢大楼(DE)的顶部竖有一块“江魂秘境,水韵方舟”的宣传牌CD,其宽度为2m,小明在平地上的A处,测得宣传牌的底部D的仰角为60°;又沿着EA的方向前进了22m到B处,测得宣传牌的底部D的仰角为45°(A、E之间有一条河),求这幢大楼DE的高度.(测角器的高度忽略不计,结果精确到0.1m.参考数据: 1.414,
1.414, 1.732)
1.732)
动手操作(本小题满分7分)
如图在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=∠ ,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);
,点B、C、D在直线l上,按下列要求画图(保留画图痕迹);
(1)画出点E关于直线l的对称点E’,连接CE’、DE’;
(2)以点C为旋转中心,将(1)中所得△CDE’ 按逆时针方向旋转,使得CE’与CA重合,
得到△CD’E’’(A).画出△CD’E’’(A).解决下面问题:
①线段AB和线段CD’的位置关系是 ▲ ;理由是: ▲ .
②求∠ 的度数.
的度数.
活动探究(本小题满分7分)
如图,已知二次函数 ,将
,将 轴下方的图象沿
轴下方的图象沿 轴翻折,得到一个新图象(图中的实线).
轴翻折,得到一个新图象(图中的实线).
根据新图像回答问题:
(1)当x= ▲ 时,函数y有最小值.
(2)当y随x的增大而增大时,自变量x的范围是 ▲ .
(3)当a<4时,探究一次函数 的图像与新图象公共点的个数情况.
的图像与新图象公共点的个数情况.
实践应用(本小题满分8分)
已知A、B两地相距300千米,甲、乙两车同时从 地出发,以各自的速度匀速往返两地.甲车先到达
地出发,以各自的速度匀速往返两地.甲车先到达 地,停留1小时后按原路返回.设两车行驶的时间为
地,停留1小时后按原路返回.设两车行驶的时间为 小时,离开
小时,离开 地的距离是
地的距离是 千米,如图是
千米,如图是 与
与 的函数图象.
的函数图象.
(1)计算甲车的速度为 ▲ 千米/时,乙车的速度为 ▲ 千米/时;
(2) 几小时后两车相遇;
(3) 在从开始出发到两车相遇的过程中,设两车之间的距离为 千米,乙车行驶的时间为
千米,乙车行驶的时间为 小时,求
小时,求 与
与 之间的函数关系式.
之间的函数关系式.
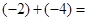 ▲ ,
▲ ,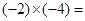 ▲ .
▲ . 的相反数是 ▲ ,-
的相反数是 ▲ ,- = ▲ ,计算
= ▲ ,计算 = ▲ .
= ▲ . 的值等于零,则
的值等于零,则 = ▲ ,当
= ▲ ,当 时,代数式
时,代数式 ,∠1=60°,∠2=50°,则∠3= ▲ 度,∠4= ▲ 度.
,∠1=60°,∠2=50°,则∠3= ▲ 度,∠4= ▲ 度.
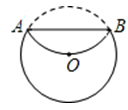
 的两根为
的两根为 ,则
,则 ▲ .
▲ .
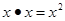
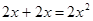
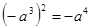
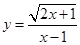 的自变量
的自变量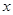 的取值范围是( ▲ )
的取值范围是( ▲ ) 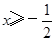
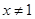
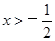 且
且 时
时 值随
值随 值增大而减小的是( ▲ )
值增大而减小的是( ▲ ) 



 的值( ▲ )
的值( ▲ )


 ,然后选择一个合适的
,然后选择一个合适的 的值代入上式求值.
的值代入上式求值. ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来. 

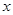 轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作
轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作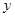 轴的垂线,两直线交于点D,直线DB交
轴的垂线,两直线交于点D,直线DB交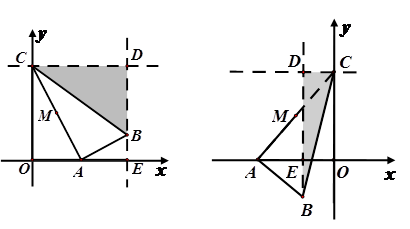
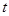 ,
,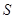 ,则
,则 ?
? 粤公网安备 44130202000953号
粤公网安备 44130202000953号