[安徽]2011—2012学年安徽滁州八年级第二学期期末数学试卷C(沪科版)
如图,每个小正方形的边长为1,A、B、C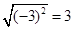 是小正方形的顶点,则∠ABC的度数为( )
是小正方形的顶点,则∠ABC的度数为( )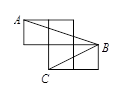
A.90° B.60° C.45° D.30°
如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是
| A.邻边相等的矩形是正方形 | B.对角线相等的菱形是正方形 |
| C.两个全等的直角三角形构成正方形 | D.轴对称图形是正方形 |
如图,梯形ABCD的对角线交于O点,△ABO和△DCO的面积分别记为S1、S2,那么下列结论正确的是 
| A.S1=S2 | B.S1>S2 |
| C.S1<S2 | D.只有当ABCD是等腰梯形是才有S1=S2 |
某校八年级有15名同学参加百米竟赛,预赛成绩各不相同,要取前8名参加决赛,小明已经知道了自己的成绩,但不知道其它人的成绩,她急着想知道自己能否进入决赛,还需要知道这15名同学成绩的( )
| A.平均数 | B.中位数 | C.众数 | D.极差 |
如图,在△ABC中,∠BAC的平分线AD=10,AC=8,CD=6,则点D到AB边的距离是( )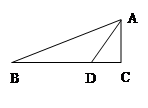
| A.8 | B.7 | C.6 | D.无法确定 |
如图,在矩形ABCD中,AB=8,BC=6,EF经过对角线的交点O,则图中阴影部分的面积是( )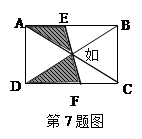
| A.6 | B.12 | C.15 | D.24 |
摄影兴趣小组的学生,将自己拍摄的照片向本组其他成员各赠送一张,全组共互赠了182张,若全组有x名学生,则根据题意列出的方程是( )
| A.x(x+1)=182 | B.0.5x(x+1)=182 |
| C.0.5x(x-1)=182 | D.x(x-1)=182 |
在平行四边形ABCD中,对角线AC,BD的长度分别为10和6,则AB长度的最大整数值是( )
| A.8 | B.5 | C.6 | D.7 |
若 、
、 是一元二次方程
是一元二次方程 的两个根,那么
的两个根,那么 的值是( )
的值是( )
| A.-2 | B.4 | C.0.25 | D.-0.5 |
如图,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,再以A1B1C1D1各边的中点为顶点作四边形 ,……,如此下去,得到四边形
,……,如此下去,得到四边形 ,若ABCD对角线长分别为a和b,请用含a、b的代数式表示四边形
,若ABCD对角线长分别为a和b,请用含a、b的代数式表示四边形 的周长 .
的周长 .
某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计结果如下:
经过计算,甲进球的平均数为 和方差
和方差 。
。
(1)求乙进球的平均数 和方差
和方差 ;(2)现在需要根据以上结果,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?为什么?
;(2)现在需要根据以上结果,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?为什么?
已知关于x的一元二次方程x2 = 2(1-m)x-m2 的两实数根为x1,x2.
(1)求m的取值范围;
(2)设y = x1 + x2,当y取得最小值时,求相应m的值,并求出最小值.
如图,在直角梯形 中,
中,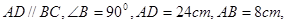
 ,动点
,动点 从
从 开始沿
开始沿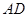 边向
边向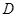 以
以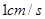 的速度运动;动点
的速度运动;动点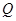 从点
从点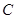 开始沿
开始沿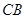 边向
边向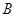 以
以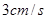 的速度运动。
的速度运动。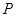 、
、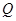 分别从点
分别从点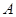 、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为
、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为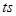 。
。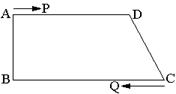
(1)当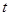 为何值时,四边形
为何值时,四边形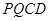 平行为四边形?
平行为四边形?
(2)当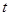 为何值时,四边形
为何值时,四边形 为等腰梯形?
为等腰梯形?
如图,在梯形ABCD中,AD∥BC,E是BC上的一点,且CE=8,BC=12,CD=4 ,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
,∠C=30°,∠B=60°。点P是线段BC边上一动点(包括B、C两点),设PB的长是x。
(1)当x为何值时,以点P、A、D、E为顶点的四边形为直角梯形。
(2)当x为何值时,以点P、A、D、E为顶点的四边形为平行四边形。
(3)P在BC 上运动时,以点P、A、D、E为顶点的四边形能否为菱形。
已知关于x的方程
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长 ,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。
,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。




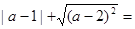 。
。
 的解,则这个三角形的周长是______。
的解,则这个三角形的周长是______。 


 、
、 如图放置,
如图放置, .求证:四边形
.求证:四边形 为菱形.
为菱形.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号