[福建]2012届福建永安九年级学业质量检测考试数学试卷
据中新社报道:2012年我国粮食产量将达到570000000吨,570000000用科学记数法表示正确的是( ▲ )
| A.5.7×107 | B.5.7×108 | C.5.7×109 | D.0.57×1010 |
如图,已知∠1 = 70º,如果CD∥BE,那么∠B的度数为( ▲)

| A.70º | B.100º |
| C.110º | D.120º |
下列调查中,适合进行普查的是( ▲ )
| A.一个班级学生的体重 | B.我国中小学生喜欢上数学课的人数 |
| C.一批灯泡的使用寿命 | D.《新闻联播》电视栏目的收视率 |
在平面直角坐标系中,点P(2,-m2-1)(m是实数)在( ▲ )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
如图,在平面直角坐标系的第一象限中有一个5×5的方形网格,每个小正方形的边长均为1个单位长,反比例函数 的图象的一个分支刚好经过四个格点(小正方形的顶点),则k=( ▲ )
的图象的一个分支刚好经过四个格点(小正方形的顶点),则k=( ▲ )
| A.2 | B.3 |
| C.5 | D.6 |
某射击队要从四名运动员中选拔一名运动员参加比赛,选拔赛中每名队员的平均成绩  与方差s2如右表所示,如果要选择一个成绩高且发挥稳定的人参赛,则这个人应是 ▲ 。
与方差s2如右表所示,如果要选择一个成绩高且发挥稳定的人参赛,则这个人应是 ▲ 。
如图,等腰直角三角形ABC的直角边AB的长为3cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中阴影部分面积等于___▲____cm2.
将1、 、
、 、
、 按右侧方式排列.若规定(m,n)表示第m排从左向右第n数,则(5,4)与(9,4)表示的两数之积是 ▲ .
按右侧方式排列.若规定(m,n)表示第m排从左向右第n数,则(5,4)与(9,4)表示的两数之积是 ▲ .
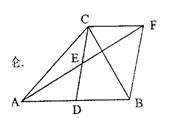
如图,在△ABC中,D是AB的中点,E是CD的中点,过点C作CF∥AB交AE的延长线于点F,连结BF。求证:△ADE≌△FCE;
若AC=BC,试判断四边形BDCF的形状,并证明你的结论。
永安市2012年初中毕业升学体育考试每位考生需考三项:50米跑为必考项目,另从立定跳远、实心球、1分钟跳绳和1分钟仰卧起坐中任选两项考试。每位考生可以根据自身条件选择不同的考试方案,如小敏选择的方案是:50米跑---立定跳远---1分钟跳绳每位考生有___▲__种选择方案;
用画树状图或列表的方法求小明与小刚选择同种方案的概率.
(友情提醒:各种方案用a、b、c、…或①、②、③、…等符号来代表可简化解答过程)。将三项考试成绩转化成等级成绩后,某校今年体育考试成绩的统计图如右图所示。则该校学生体育考试成绩的中位数落在 ▲ 级内

如图,以AB为直径的⊙O经过点C,D是AB延长线上一点,且DC=AC,∠CAB=30°试判断CD所在的直线与⊙O的位置关系,并说明理由
若AB=2,求阴影部分的面积

某校八年级举行演讲比赛,派了两位老师去学校附近的超市购买笔记本作为奖品。经过了解得知,该超市的A,B两种笔记本的价格分别是12元和8元,他们准备购买这两种笔记本共30本。如果他们计划用300元购买奖品,那么能买这两种笔记本各多少本?
两位老师根据演讲比赛的设奖情况,决定所购买的A种笔记本的数量不少于B种笔记本数量的
 ,如果设他们买A种笔记本n本,买这两种笔记本共花费w元。
,如果设他们买A种笔记本n本,买这两种笔记本共花费w元。
①请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
②请你帮他们计算,购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边长与腰长的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA= 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
计算:sad60°= ▲
对于0°<A<90°,∠A的正对值sadA的取值范围是 ▲ ;
如图2,已知△DEF中,∠E=90°,cosD=
 ,试求sadD的值。
,试求sadD的值。




 的解集在数轴上表示正确的是( ▲ )
的解集在数轴上表示正确的是( ▲ )






 记作
记作 ,则向北走
,则向北走 记作 ▲
记作 ▲  .
. = ▲ .
= ▲ .



 粤公网安备 44130202000953号
粤公网安备 44130202000953号