[广东]2011-2012学年广东省茂名市茂港区七年级下学期期中考试数学卷
下列运算正确的是( )
| A.a2•a3=a6 | B.(a2)3=a6 | C.a6÷a2=a3 | D.2﹣3=﹣6 |
下列各数据中,是近似数的有( )
①小明的身高是183.5米;②小明家买了100斤大米;③小明买笔花了4.8元; ④小明的体重是70千克。
| A.1个 | B.2个 | C.3个 | D.4个 |
下列说法正确是 ( )
| A.4不是单项式 | B. 的系数是2 的系数是2 |
C. 的次数是3 的次数是3 |
D. 的次数是3. 的次数是3. |
下列说法中,正确的是 ( )
| A.一个角的补角一定比这个角大 |
| B.一个角的余角一定比这个角小 |
| C.一对对顶角的两条角平分线必在同一条直线上 |
| D.有公共顶点并且相等的两个角是对顶角。 |
2008年北京承办奥运会取得圆满成功。据统计某日奥运会网站的访问人次为201949,用四舍五入法取近似值保留两个有效数字,得( )
| A.2.0×105 | B.2.0×106 | C.2×105 | D.0.2×106 |
如图,直线l与直线a、b相交,且a∥b,∠1=80°, 则∠2的度数是( )
| A.60° | B.80° |
| C.100° | D.120° |
如图所示,从边长为a的大正方形中挖去一个边长是b的小正方形,小明将图甲中的阴影部分拼成了一个如图乙所示的矩形,这一过程可以验证( )
| A.a2+b2-2ab=(a-b)2 | B.a2+b2+2ab=(a+b)2 |
| C.2a2-3ab +b2=(2a-b)(a-b) | D.a2-b2=(a+b(a-b) |
某商场为吸引顾客设计了如图所示的自由转盘,当指针指向阴影部分是,该顾客可获奖品一份,那么该顾客获奖的概率为 ( )
A. |
B. |
C. |
D. |
观察下列顺序排列的等式:
9×0+1=1
9×1+2=11
9×2+3=21
9×3+4=31
9×4+5=41
……
根据数表所反映的规律,猜想:第n个等式(n为正整数)应为( )
A.9(n-1)+n="10" (n-1)+1 B.9n+n=(n-1)+1
C.9n+(n-1)=n2-1 D. 9n+n+1=10n+1
任意掷一枚均匀的,每个面分别标有数字1,2,3,4,5,6的小正方体,则出现奇数朝上的概率为 .
找规律,如图有大小不同的平行四边形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n幅图中有 个。
作图题(尺规作图,不写作法,但保留作图痕迹)
如图,已知,∠α 、∠β。
求作∠AOB,使∠AOB =2∠α+∠β,
推理填空,如图
1、 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
 是三个连续的正整数
是三个连续的正整数 ,以b为边长作正方形,分别以c,
,以b为边长作正方形,分别以c, 为长和宽作长方形,哪个图形的面积大?为什么?
为长和宽作长方形,哪个图形的面积大?为什么?
按下面的方法折纸,然后回答问题:
(1)∠2是多少度的角?为什么?
(2)∠1与∠3有何关系?
(3)∠1与∠AEC,∠3与∠BEF分别有何关系?
如图,某电视台的娱乐节目《周末大放送》有这样的翻奖牌游戏,数字的背面写有祝福语或奖金数,游戏规则是:每翻动正面一个数字,看看反面对应的内容,就可知是得奖还是得到温馨祝福。
计算:
(1)“翻到奖金1000元”的概率;
(2)“翻到奖金”的概率;
(3)“翻不到奖金”的概率。
如图①是一个长为2a,宽为2b的长方形,沿图中虚线剪开,将其分成4个小长方形,然后按图②的形状拼成一个正方形。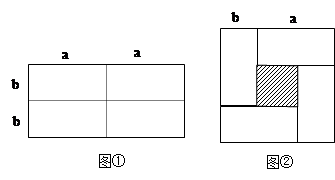
1、图②中阴影部分的正方形的边长等于多少?
2、用两种不同的方法求图②中阴影部分的面积。
3、由图②你能写出下列三个代数式间的关系吗?
(a+b)2,(a-b)2,4ab

 = 。
= 。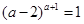 ,则a= 。
,则a= 。 ,其中
,其中
 粤公网安备 44130202000953号
粤公网安备 44130202000953号