[四川]2010-2011学年达州市高中阶段教育学校招生统一考试数学卷
生活处处皆学问.如图1,自行车轮所在两圆的位置关系是
| A.外切 | B.内切 |
| C.外离 | D.内含 |
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为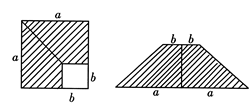
A.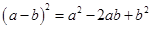 |
B.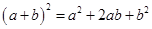 |
C. |
D.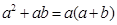 |
在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
① ,如
,如 ;
;
② ,如
,如 .
.
按照以上变换有: ,那么
,那么 等于
等于
| A.(3,2) | B.(3,-2) |
| C.(-3,2) | D.(-3,-2) |
如图,在一块形状为直角梯形的草坪中,修建了一条由A→M→N→C的小路(M、N分别是AB、CD中点).极少数同学为了走“捷径”,沿线段AC行走,破坏了草坪,实际上他们仅少走了图4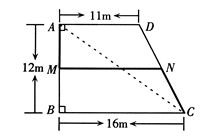
A. 7米 B. 6米
C. 5米  D. 4米
D. 4米
大巴山隧道是达陕高速公路中最长的隧道,总长约为6000米,这个数据用科学记数法表示为 米.
在“讲政策、讲法制、讲道德、讲恩情”的演讲比赛中,五位选手的成绩如下:
这组成绩的极差是 分.
请写出符合以下两个条件的一个函数解析式 .
过点(-2,1), ②在第二象限内,y随x增大而增大.
如图6,一个宽为2 cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是 cm.
上海世博会自开幕以来,前往参观的人络绎不绝.柳柳于星期六去参观,她决定上午在三个热门馆:中国馆(A),阿联酋馆(B),英国馆(C)中选择一个参观,下午在两个热门馆:瑞士馆(D)、非洲联合馆(E)中选择一个参观.请你用画树状图或列表的方法,求出柳柳这一天选中中国馆(A)和非洲联合馆(E)参观的概率是多大?(用字母代替馆名)[
如图,将一矩形纸片ABCD折叠,使点C与点A重合,点D落在点E处,折痕为MN,图中有全等三角形吗?若有,请找出并证明.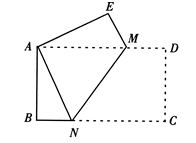
在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.
方案是否符合条件有不同意见,你认为小芳的方案符合条件吗?若不符合,请用方程的方法说明理由.你还有其他的设计方案吗?请在图9-3中画出你所设计的草图,将花园部分涂上阴影,并加以说明.

已知:如图,AB和DE是直立在地面上的两根立柱,AB="5" m,某一时刻,AB在阳光下的投影BC="4" m.
请你在图中画出此时DE在阳光下的投影,并简述画图步骤;
在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图,根据题中相关信息回答下列问题: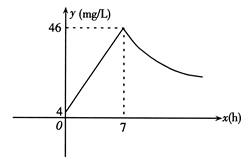
求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
矿工只有在空气中的CO浓度
 降到4 mg/L
降到4 mg/L 及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井?
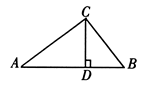
已知:如图,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN于F.
猜想ED与⊙O的位置关系,并说明理由;
若cos∠MAN=
 ,AE=
,AE= ,求阴影部分的面积.
,求阴影部分的面积.

 中自变量的取值范围在数轴上表示为
中自变量的取值范围在数轴上表示为





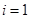 ︰
︰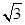 ,则该坡的坡角
,则该坡的坡角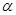 = .
= .
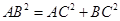
 ④
④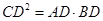
 .
. 和
和 ,你能找到一个合适的
,你能找到一个合适的 值,使它们的值相等吗?写出你的解题过程.
值,使它们的值相等吗?写出你的解题过程. 的抛物线
的抛物线 与
与 轴相交于点
轴相交于点 、
、 .
.
 的坐标;
的坐标; ,当0<S≤18时,求
,当0<S≤18时,求 ,使△OP
,使△OP 粤公网安备 44130202000953号
粤公网安备 44130202000953号