[河北]2011-2012年河北省衡水市五校九年级第三次联考数学卷
若△ABC~△DEF,它们的面积比为4︰1,则△ABC与△DEF的相似比为( )
| A.2︰1 | B.1︰2 | C.4︰1 | D.1︰4 |
若二次函数y=x2-6x+c的图像过A(-1,y1),B(2,y2),C(5,y3),则y1,y2,
y3的大小关系是( )
| A.y1>y2>y3 | B.y1>y3>y2 | C.y2>y1>y3 | D.y3>y1>y2 |
已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )
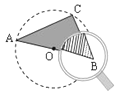 |
A.∠A=∠B B.∠A+∠B=90°
C.∠A+∠B>90° D.∠A+∠B的值无法确定
如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
| A.600m | B.500m | C.400m | D.300m |
由函数y=-12x2的图像平移得到函数y=-12(x-4)2+5的图像,则这个平移是( )
| A.先向左平移4个单位,再向下平移5个单位 |
| B.先向左平移4个单位,再向上平移5个单位 |
| C.先向右平移4个单位,再向下平移5个单位 |
| D.先向右平移4个单位,再向上平移5个单位 |
阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE,(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )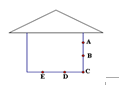
| A.4米 | B.3.8米 | C.3.6米 | D.3.4米 |
已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图像如图所示, 有下列结论:①abc>0,②b2-4ac<0,③a-b+c>0,④4a-2b+c<0, 其中正确结论的个数是( )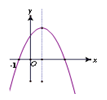
| A.1 | B.2 | C.3 | D.4 |
如图,P为线段AB上一点,AD与BC交于E,∠CPD=∠A=∠B, BC交PD于F,AD交PC于G,则图中相似三角形有( )
| A.1对 | B.2对 | C.3对 | D.4对 |
如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,依次类推,若各种开本的矩形都相似,那么 等于( )
等于( )
| A.0.618 | B.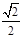 |
C. |
D.2 |
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,
垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图像是( )
已知抛物线y=(m-1)x2,且直线y=3x+3-m经过一、二、三象限,则m的范围是 m≠1且m<3 。
在比例尺为1︰200的地图上,测得A、B两地间的图上距离为4.5cm,则A、B两地间的实际距离为 9m。
数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米,同时另一名同学测量一棵树的高 度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地
度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地 面上的影长为2.4米,则树高为 4.2米。
面上的影长为2.4米,则树高为 4.2米。
如图是抛物线y=ax2+bx+c的一部分,其对称轴为直线x=1,若其与x轴一交点为B
(3,0),则由图像可知,不等式ax2+bx+c>0的解集是 x<-1或x>3。
已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如图示)。当n=8时,共向外做出了 18个小等边三角形; 当n=k时,共向外做出了 3(k-2)个小等边三角形,这些小等边三角形的面积和是 3(k-2)k2S(用含k的式子表示)。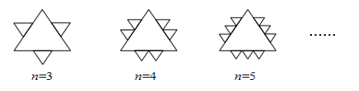
(本小题满分6分)计算:已知二次函数 。
。(1)画出图像,指出对称轴,顶点,求出何时y随x的增大而减小;
(2)写出不等式
 ≥0的解集。
≥0的解集。
(本小题满分6分)如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE。
(1)写出图中两对相似三角形(不得添加辅助线);
(2)请分别说明两对三角形相似的理由。
(本小题满分8分)在直角坐标系中,已知点A(-2,0)、 B(0,4)、C(0,3),过点C作直线交x轴于点D,使得以 D、O、C为顶点的三角形与△AOB相似,求点D的坐标。
B(0,4)、C(0,3),过点C作直线交x轴于点D,使得以 D、O、C为顶点的三角形与△AOB相似,求点D的坐标。
(本小题满分9分)深圳大运会期间,某宾馆有若干间住房,住宿记录提供了如下信息:①7月20日全部住满,一天住宿费收入为3600元;②7月21日有10间房空着,一天住宿费收入为2800元;③该宾馆每间房每天收费标准相同。(1)求该宾馆共有多少间住房,每间住房每天收费多少元?
(2)通过市场调查发现,每个住房每天的定价每增加10元,就会有一个房间空闲
 ;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
(1)求经过A、B、C三点的抛物线的表达式;
(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1
与△OAB对应线段的比为3:1,请在右图网格中画出放大
后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平
移得到?请说明理由。
.(本小题满分9分)如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题: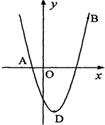
(1)求抛物线的解析式;
(2)若抛物线的顶点为点D,对称轴所在的直线交x轴于点E,
连接AD,点F为AD的中点,求出线段EF的长。
注:抛物线y=ax2+bx+c的对称轴是x= ,顶点坐标是
,顶点坐标是
( ,
, )。
)。
(本小题满分12分)某班同学到野外活动,为测量一池塘两端A、B的距离,设计了几种方案,下面介绍两种:(I)如图(1),先在平地取一个可以直接到达A、B的点C,并分别延长AC到D,BC到E,使DC=AC,BC=EC,最后测出DE的距离即为AB的长。(II)如图(2),先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离。阅读后回答下列问题:
(1)方案(I)是否可行?为什么?
(2)方案(II)是否切实可行?为什么?
(3)方案(II)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°,方案(II)是否成立?
(4)方案(II)中,若使BC=n·CD,能否测得(或求出)AB的长?理由是 ,若ED=m,则AB= 。
(本小题满分12分)
如图(1),△ABC与△ EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止。不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2)。
EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止。不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2)。
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由);
(3)问:当x为何值时,△AGH是等腰三角形?


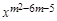 是二次函数,则m的值为 。
是二次函数,则m的值为 。 粤公网安备 44130202000953号
粤公网安备 44130202000953号