[江苏]2011-2012年江苏省阜宁县部分初中九年级联考数学卷

下列图形中不是中心对称图形的是【  】

下列成语所描述的事件是必然发生的事件是【  】

如果有意义，那么字母的取值范围是【  】

A．

B．

C．

D．

已知正三角形的边长为12，则这个正三角形外接圆的半径是

A．

B．

C．

D．

如图，点A、C、B在⊙O上，已知∠AOB =∠ACB =α．则α的值为【  】

如图,⊙O的半径为5，弦AB=8，M是弦AB上的动点，则OM不可能为【  】

若是方程的一个根，则代数式的值等于【  】

设表示不超过x的最大整数，如=1，=3，……
那么等于【  】

一元二次方程的两根分别为【  】

把方程配方，化为的形式应为【  】

A．

B．

C．

D．

已知⊙O₁的半径为2cm，⊙O₂的半径为3cm，两圆的圆心距为5cm，则⊙O₁和⊙O₂的位置关系为         

直径12cm的圆中，垂直平分半径的弦长为           cm．

已知,,则=          

若成立，则        

关于x的方程,当=     时为一元二次方程．

如图，直角坐标系中一条圆弧经过网格点A，B，C，其中B点坐标为（4，4），则该弧所在圆心的坐标是           ．

如图，等边三角形ABC的边长为2cm，D、E分别是AB、AC上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分图形的周长为       cm．

如图，正方形A₁B₁C₁O，A₂B₂C₂C₁，A₃B₃C₃C₂，…按照如图所示的方式放置，点A₁，A₂，A₃，…和点C₁，C₂，C₃，…分别在直线和x轴上，已知点B₁（1，1），B₂（3，2），则B₃的坐标是        

(10分)．解方程
（1）           
（2）

计算
（1）             
（2）

已知在平面直角坐标系中的位置如下图所示．

（1）分别写出图中点的坐标；
（2）画出绕点按逆时针方向旋转后的；
（3）求点旋转到点所经过的路线长（结果保留）．

如图，ABCD是围墙，AB∥CD，∠ABC=120°，一根6m长的绳子，一端拴在围墙一角的柱子上（B处），另一端拴着一只羊（E处）．

（1）请在图中画出羊活动的区域．
（2）求出羊活动区域的面积．

已知a、b、c均为实数，且，求方程的根．

(10分)观察下列等式：
①； ②；③；……
回答下列问题：
（1）利用你观察到的规律，化简：
（2）计算：

如图，PA，PB是⊙O的切线，点A，B为切点，AC是⊙O的直径，∠ACB=70°．求∠P的度数．

如图，在直角梯形ABCD中，AB∥DC，∠D = 90^o，AC⊥BC，
AB =" 10cm" , BC = 6cm，F点以2 cm／秒的速度在线段AB上由A向B匀速运动， E点同时以1 cm／秒的速度在线段BC上由B向C匀速运动，设运动时间为 t 秒 ( 0 < t < 5 )．

（1）求证：△ A C D ∽△ B A C ；
（2）求DC的长；
（3）设四边形AFEC的面积为 y ，求 y关于t的函数关系式．

李明的爸爸从市场上卖回来一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1m的正方形后，剩下的部分刚好能围成一个容积为15m³的无盖长方体运输箱，且此长方体运输箱底面的长比宽多2m，现已知购买这种铁皮每平方米需30元，问李明爸爸购回这张矩形铁皮共花了多少钱？

如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．

（1）在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的；
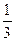（2）在点P的运动过程中，是否存在某一时刻，⊙A与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．