[浙江]2011-2012年浙江省温岭市八年级第一学期四校期中联考数学卷
一个数的立方根等于它本身,则这个数是 ( ).
| A.0 | B.±1 | C.1 | D.0,±1 |
如果等腰三角形的两边长分别是4和5,则它的周长是( ).
| A.13 | B.14 | C.13或14 | D.无法确定 |
下列叙述正确的语句是( ).
| A.无限小数是无理数 | B.等腰三角形的高、中线、角平分线互相重合 |
| C.全等三角形对应边上的高相等 | D.两腰相等的两个等腰三角形全等 |
如图 , 在∠AOB的两边上截取AO="BO" , 点C、D在AO和BO上,下列条件中不能判定△AOD≌△BOC的是 ( ).
A.∠A=∠B B.OC=OD C. AC=BD D. AD=BC
等腰三角形的一个外角是80°,则其底角是( ).
| A.100° | B.100°或40° | C.40° | D.80° |
如图,已知MN是△ABC边AB的垂直平分线,垂足为F,AD是∠CAB的平分线,且MN与AD交于O点。连接BO并延长交AC于E,则下列结论中,不一定成立的是( ).
| A.∠CAD=∠BAD | B.OE=OF |
| C.AF=BF | D.OA="OB" |
如图是一个等边三角形木框,甲虫P在边框AC上爬行(A、C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( )
.
A.d>h B.d<h C.d=h D.无法确定
如右图所示,在△ABC中,∠A=90°,BD平分∠ABC,AD=2 cm,则点D到BC的距离为________cm.
在平面直角坐标系中,O为坐标原点,已知点A(2,-2),在 轴上确定点P,使△AOP为等腰三角形,则符合条件的有_______个.
轴上确定点P,使△AOP为等腰三角形,则符合条件的有_______个.
如右图,已知BO平分∠CBA,CO平分∠ACB,MN∥BC,且过点O,若AB=12,AC=14,则△AMN的周长是 .
如右图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好在BC上,则AP的长是 .
如图,点B、E、C、F在一条直线上,BC="EF " AB∥DE,请你添加一个条件 ,使△ABC≌△DEF。并写出证明过程.
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3) 
(1)求出 的面积.
的面积.
(2)在图中作出 关于
关于 轴的对称图形
轴的对称图形 .
.
(3)写出点 的坐标.
的坐标.
在ABC中,AB=AC,∠BAC=120°,AD⊥AC于点A,
(1)求∠BAD的度数.
(2)证明:DC=2BD.
阅读下列材料,并回答问题.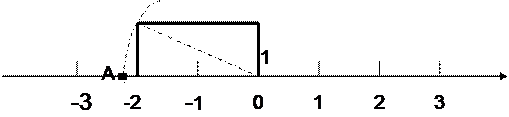
画一个直角三角形,使它的两条直角边分别为5和12,那么我们可以量得直角三角形的斜边长为13,并且 。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则
。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则 ,这个结论就是著名的勾股定理.
,这个结论就是著名的勾股定理.
请利用这个结论,完成下面的活动:
(1)一个直角三角形的两条直角边分别为6、8,那么这个直角三角形斜边长为 .
(2)满足勾股定理方程 的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
① 3, 4, 5 ; ② 5,12,13 ; ③ 7,24,25 ;④ 9,40,41 ;
请你写出有以上规律的第⑤组勾股数: .
(3)如图,AD⊥BC于D,AD=BD,AC=BE。AC=3,DC=1,求BD的长度.
(4)如图,点A在数轴上表示的数是 ,请用类似的方法在下图数轴上画出表示数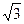 的B点(保留作图痕迹).
的B点(保留作图痕迹).




 表示的数可能是( ).
表示的数可能是( ).







 ,则
,则 .
. +
+ —
— (2)求x的值:
(2)求x的值:

 粤公网安备 44130202000953号
粤公网安备 44130202000953号