[海南]2011年海南省海口市初三学业模拟考试数学卷
数据2500000用科学记数法表示为
| A.25×105 | B.2.5×105 | C.2.5×106 | D.2.5×107 |
如图1,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=28°,则∠2等于
| A.52º | B.60º | C.62º | D.72º |
 |
如图2,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,若CD=2,则点D到AB的距离是( )
| A.1 | B.2 | C.3 | D.4 |

如图3,在△ABC中,DE∥BC,DB=2AD,DE=4,则BC边的长等于
| A.6 | B.8 | C.10 | D.12 |
 |
如图4,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1等于
| A.100° | B.110° | C.120° | D.130° |
 |
如图6,⊙O的直径AB垂直于弦CD,垂足为E,若∠BAD=20°,则∠BOC等于
| A.20° | B.40° | C.50° | D.60° |
 |
袋中有5个白球,x个红球,从中随机摸出一个球,恰为红球的概率为 ,则x为
,则x为
| A.25 | B.20 | C.15 | D.10 |
已知一次函数y=kx+b(k≠0,k,b为常数),x与y的部分对应值如下表所示
则不等式kx+b<0的解集是
| A.x>1 | B.x<1 |
| C.x>0 | D. x<0 |
如图7,矩形纸片ABCD,AB=6,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B的对应点B′恰好落在AC上,则AC的长是 .
 |
(满分8分)某市为治理污水,需要铺设一段全长为300米的污水排放管道.铺设120米后,为了尽量减少施工对城市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用15天完成这一任务.求原计划每天铺设管道的长度.
(满分8分)为了解某中学九年级学生中考体育成绩情况,现从中抽取部分学生的体育成绩进行分段(A:50分、B:49~40分、C:39~30分、D:29~0分)统计,统计结 果如图9.1、图9.2所示.
果如图9.1、图9.2所示.
 |
根据上面提供的信息 ,回答下列问题:
,回答下列问题:
(1)本次抽查了多少名学生的体育成绩;
(2)补全图9.1,求图9.2中D分数段所占的百分比;
(3)已知该校九年级共有900名学生, 请估计该校九年级学生体育成绩达到40分以上(含40分)的人数.
请估计该校九年级学生体育成绩达到40分以上(含40分)的人数.
(满分8分)在如图10所示的正方形网格中,△ABC的顶点均在格点上,在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C,并写出点B2的坐标;
(3)把△ABC 以点A为位似中心放大,使放大前后对应边长的比为1:2,画出放大后的△AB3C3.
以点A为位似中心放大,使放大前后对应边长的比为1:2,画出放大后的△AB3C3.
(满分11分)如图11,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于F,连结CF.
(1)求证:AF=CD;
(2)若AB=AC,∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,求sin∠ABF的值.
 |
(满分13分)如图12.1,已知抛物线经过坐标原点O和x轴上另一点E(4,0),顶点M的坐标为 (m,4),直角梯形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且BC=1,AD=2,AB=3.
(1)求m的值及该抛物线的函数关系式;
(2)将直角梯形ABCD以每秒1个单位长度的速度从图12.1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向点B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图12.2所示).
①当t为何值时,△PNC是以PN为底边的等腰三角形;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说 明理由.
明理由.
 |
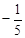
 又是中心对称图形的是
又是中心对称图形的是
 的解是
的解是



 图象上的点是
图象上的点是 ,1)
,1) 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是 的边OA上一点,且点P的坐标为(4,3),则cos
的边OA上一点,且点P的坐标为(4,3),则cos





 )2+
)2+ ×(-
×(- )+(
)+( )0 ;(2)化简:
)0 ;(2)化简: .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号