[河南]2012届河南省卢氏一高高三适应性考试理科数学
“若一个数不是负数,则它的平方不是正数”和这个命题真值相同的命题为( )
| A.若一个数是负数,则它的平方是正数 | B.若一个数的平方不是正数,则它不是负数 |
| C.若一个数的平方是正数,则它是负数 | D.若一个数不是负数,则它的平方是非负数 |
若非空集合S {1,2,3,4,5},且若a∈S,则必有6-a∈S,则所有满足上述条件的集合S共有( )
{1,2,3,4,5},且若a∈S,则必有6-a∈S,则所有满足上述条件的集合S共有( )
| A.6个 | B.7个 | C.8个 | D.9个 |
f(x)是定义域为R的增函数,且值域为R+,则下列函数中为减函数的是( )
| A.f(x)+ f(-x) | B.f(x)-f(-x) |
| C.f(x)·f(-x) | D. |
函数f(x)=x2+ax-3a-9对任意x∈R恒有f(x)≥0,则f(1)=( )
| A.6 | B.5 | C.4 | D.3 |
关于x的方程ax=-x2+2x+a(a>0,且a≠1)的解的个数是( )
| A.1 | B.2 | C.0 | D.视a的值而定 |
当x∈(-2,-1)时,不等式(x+1)2<loga|x|恒成立,则实数a的取值范围是( )
| A.[2,+∞) | B.(1,2] |
| C.(1,2) | D.(0,1) |
对于函数 则下列正确的是( )
则下列正确的是( )
| A.该函数的值域是[-1,1] |
B.当且仅当 时,该函数取得最大值1 时,该函数取得最大值1 |
C.当且仅当 |
| D.该函数是以π为最小正周期的周期函数 |
设平面上有四个互异的点A、B、C、D,已知( 则△ABC的形状是( )
则△ABC的形状是( )
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
(本小题满分10分)设a、b∈Z,E={(x,y)|(x-a)2+3b≤6y},点(2,1)∈E,但(1,0) E,(3,2)
E,(3,2) E。求a、b的值。
E。求a、b的值。
(本小题满分12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数
(1)当0≤x≤200时,求函数v(x)的表达式
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
(本小题满分12分)设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
(1)求证:f(0)=1,且当x<0时,有f(x)>1;
(2)判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B= ,求a的取值范围。
,求a的取值范围。
 ?,则lg
?,则lg +lg
+lg 的值是( )
的值是( ) 的值的范围是( )
的值的范围是( )


 的大致图象,
的大致图象, 等于( )
等于( )





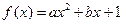 的导函数为
的导函数为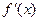 ,
, ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则 的最小值为( )
的最小值为( ) 平移后,得到的图象的表达式为
平移后,得到的图象的表达式为 ,则原函数的解析式为
,则原函数的解析式为  的零点
的零点 ,且
,且 ,
, ,
, ,则
,则
 (a≠0),若
(a≠0),若 ,x0>0,则x0=
,x0>0,则x0=  为原点,且
为原点,且 (其中
(其中 均为实数),若N(1,0),则
均为实数),若N(1,0),则 的最小值是
的最小值是  为锐角,求
为锐角,求 的值
的值
 ;
;
 和点
和点 ,过点
,过点 作曲线
作曲线 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 .
. 为关于
为关于 的方程
的方程 的两根;
的两根; ,求函数
,求函数 的表达式;
的表达式; 内总存在
内总存在 个实数
个实数 (可以相同),使得不等式
(可以相同),使得不等式 成立,求
成立,求 的最大值.
的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号