2022年中考数学专题:数据分析(二)
"杂交水稻之父"袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取9株水稻苗,测得苗高(单位: 分别是:22,23,24,23,24,25,26,23,25.则这组数据的众数和中位数分别是
| A. |
24,25 |
B. |
23,23 |
C. |
23,24 |
D. |
24,24 |
某班15名男生引体向上成绩如表:
个数 |
17 |
12 |
10 |
7 |
2 |
人数 |
2 |
3 |
4 |
5 |
1 |
则这组数据的众数和中位数分别是
| A. |
10,7 |
B. |
10,10 |
C. |
7,10 |
D. |
7,12 |
某校为了解学生的睡眠情况,随机调查部分学生一周平均每天的睡时间,统计结果如表:
时间 小时 |
7 |
8 |
9 |
10 |
人数 |
6 |
9 |
11 |
4 |
这些学生睡眠时间的众数、中位数是
| A. |
众数是11,中位数是8.5 |
B. |
众数是9,中位数是8.5 |
| C. |
众数是9,中位数是9 |
D. |
众数是10,中位数是9 |
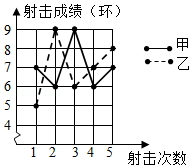
甲、乙两人进行飞镖比赛,每人各投6次,他们的成绩如下表(单位:环)
甲 |
6,7,8,8,9,9 |
乙 |
5,6, ,9,9,10 |
如果两人的比赛成绩的中位数相同,那么乙的第三次成绩 是
| A. |
6环 |
B. |
7环 |
C. |
8环 |
D. |
9环 |
下列说法正确的是
| A. |
一个不透明的口袋中有3个白球和2个红球(每个球除颜色外都相同),则从中任意摸出一个球是红球的概率为 |
| B. |
一个抽奖活动的中奖概率为 ,则抽奖2次就必有1次中奖 |
| C. |
统计甲,乙两名同学在若干次检测中的数学成绩发现: , ,说明甲的数学成绩比乙的数学成绩稳定 |
| D. |
要了解一个班有多少同学知道"杂交水稻之父"袁隆平的事迹,宜采用普查的调查方式 |
为了落实"作业、睡眠、手机、读物、体质"等五项管理要求,了解学生的睡眠状况,调查了一个班50名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为

| A. |
|
B. |
|
C. |
|
D. |
|
下列说法正确的是
| A. |
角平分线上的点到角两边的距离相等 |
| B. |
平行四边形既是轴对称图形,又是中心对称图形 |
| C. |
在代数式 , , ,985, , 中, , , 是分式 |
| D. |
若一组数据2、3、 、1、5的平均数是3,则这组数据的中位数是4 |
一组数据:2,4,4,4,6,若去掉一个数据4,则下列统计量中发生变化的是
| A. |
众数 |
B. |
中位数 |
C. |
平均数 |
D. |
方差 |
在2021年初中毕业生体育测试中,某校随机抽取了10名男生的引体向上成绩,将这组数据整理后制成如下统计表:
成绩(次 |
12 |
11 |
10 |
9 |
人数(名 |
1 |
3 |
4 |
2 |
关于这组数据的结论不正确的是
| A. |
中位数是10.5 |
B. |
平均数是10.3 |
C. |
众数是10 |
D. |
方差是0.81 |
有6位同学一次数学测验分数分别是:125,130,130,132,140,145,则这组数据的中位数是
| A. |
130 |
B. |
132 |
C. |
131 |
D. |
140 |
某中学规定学生的学期体育成绩满分为100,其中体育课外活动占 ,期末考试成绩占 ,小彤的这两项成绩依次是90,80.则小彤这学期的体育成绩是 .
开学前,根据学校防疫要求,小芸同学连续14天进行了体温测量,结果统计如表:
体温 |
36.3 |
36.4 |
36.5 |
36.6 |
36.7 |
36.8 |
天数(天 |
2 |
3 |
3 |
4 |
1 |
1 |
这14天中,小芸体温的众数是 .
为庆祝建党100周年,某校举行“庆百年红歌大赛”.七年级5个班得分分别为85,90,88,95,92,则5个班得分的中位数为 分.
甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均数都是8环,方差分别为 , ,则两人射击成绩比较稳定的是 (填“甲”或“乙” .
中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物.在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如表:
中药 |
黄芪 |
焦山楂 |
当归 |
销售单价(单位:元 千克) |
80 |
60 |
90 |
销售额(单位:元) |
120 |
120 |
360 |
则在这个时间段,该中药房的这三种中药的平均销售量为 千克.
在某次体育测试中,甲、乙两班成绩的平均数、中位数、方差如下表所示,规定学生个人成绩大于90分为优秀,则甲、乙两班中优秀人数更多的是 班.
人数 |
平均数 |
中位数 |
方差 |
|
甲班 |
45 |
82 |
91 |
19.3 |
乙班 |
45 |
87 |
89 |
5.8 |
为落实湖南省共青团“青年大学习”的号召,某校团委针对该校学生每周参加“青年大学习”的时间(单位: 进行了随机抽样调查,并将获得的数据绘制成如下统计表和如图所示的统计图,请根据图表中的信息回答下列问题.
周学习时间 |
频数 |
频率 |
|
5 |
0.05 |
|
20 |
0.20 |
|
|
0.35 |
|
25 |
|
|
15 |
0.15 |
(1)求统计表中 , 的值.
(2)甲同学说“我的周学习时间是此次抽样调查所得数据的中位数”.求甲同学的周学习时间在哪个范围内.
(3)已知该校学生约有2000人,试估计该校学生每周参加“青年大学习”的时间不少于 的人数.

某校要从甲,乙两名学生中挑选一名学生参加数学竞赛,在最近的8次选拔赛中,他们的成绩(成绩均为整数,单位:分)如下:
甲:92,95,96,88,92,98,99,100
乙:100,87,92,93,9■,95,97,98
由于保存不当,学生乙有一次成绩的个位数字模糊不清,
(1)求甲成绩的平均数和中位数;
(2)求事件“甲成绩的平均数大于乙成绩的平均数”的概率;
(3)当甲成绩的平均数与乙成绩的平均数相等时,请用方差大小说明应选哪个学生参加数学竞赛.
2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分)
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.
七八年级教师竞赛成绩统计表
年级 |
七年级 |
八年级 |
平均数 |
8.5 |
8.5 |
中位数 |
|
9 |
众数 |
8 |
|
优秀率 |
|
|
根据以上信息,解答下列问题:
(1)填空: , ;
(2)估计该校七年级120名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异.

垃圾的分类回收不仅能够减少环境污染、美化家园,甚至能够变废为宝、节约资源.为增强学生垃圾分类意识,推动垃圾分类进校园,某中学组织全校1565名学生参加了“垃圾分类知识竞赛”(满分为100分).该校数学兴趣小组为了解全校学生竞赛分数情况,采用简单随机抽样的方法(即每名学生的竞赛分数被抽到的可能性相等的抽样方法)抽取部分学生的竞赛分数进行调查分析.
(1)以下三种抽样调查方案:
方案一:从七年级、八年级、九年级中指定部分学生的竞赛分数作为样本;
方案二:从七年级、八年级中随机抽取部分男生的竞赛分数以及在九年级中随机抽取部分女生的竞赛分数作为样本;
方案三:从全校1565名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本.
其中抽取的样本最具有代表性和广泛性的一种抽样调查方案是 (填写“方案一”、“方案二”或“方案三” ;
(2)该校数学兴趣小组根据简单随机抽样方法获得的样本,绘制出如下统计表 分及以上为“优秀”,60分及以上为“及格”,学生竞赛分数记为 分)
样本容量 |
平均分 |
及格率 |
优秀率 |
最高分 |
最低分 |
100 |
83.59 |
|
|
100 |
52 |
分数段 |
|
|
|
|
|
频数 |
5 |
7 |
18 |
30 |
40 |
结合上述信息解答下列问题:
①样本数据的中位数所在分数段为 ;
②全校1565名学生,估计竞赛分数达到“优秀”的学生有 人.
某中学九年级举办中华优秀传统文化知识竞赛.用简单随机抽样的方法,从该年级全体600名学生中抽取20名,其竞赛成绩如图:

(1)求这20名学生成绩的众数,中位数和平均数;
(2)若规定成绩大于或等于90分为优秀等级,试估计该年级获优秀等级的学生人数.
国家规定“中小学生每天在校体育活动时间不低于 ”.为此,某市就“每天在校体育活动时间”的问题随机调查了辖区内部分初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
组:
组:
组:
组:

请根据上述信息解答下列问题:
(1)本次调查的人数是 人;
(2)请根据题中的信息补全频数分布直方图;
(3) 组对应扇形的圆心角为 ;
(4)本次调查数据的中位数落在 组内;
(5)若该市辖区约有80000名初中学生,请估计其中达到国家规定体育活动时间的学生人数约有多少.
2020年我国是全球主要经济体中唯一实现经济正增长的国家,各行各业蓬勃发展,其中快递业务保持着较快的增长.给出了快递业务的有关数据信息.

年快递业务量增长速度统计表
年龄 |
2016 |
2017 |
2018 |
2019 |
2020 |
增长速度 |
|
|
|
|
|
说明:增长速度计算办法为:增长速度
根据图中信息,解答下列问题:
(1) 年快递业务量最多年份的业务量是 亿件.
(2) 年快递业务量增长速度的中位数是 .
(3)下列推断合理的是 (填序号).
①因为 年快递业务量的增长速度逐年下降,所以预估2021年的快递业务量应低于2020年的快递业务量;
②因为 年快递业务量每年的增长速度均在 以上.所以预估2021年快递业务量应在 亿件以上.
某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.
(1)求考生小红和小强自选项目相同的概率;
(2)除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:

考生 |
自选项目 |
长跑 |
掷实心球 |
小红 |
95 |
90 |
95 |
小强 |
90 |
95 |
95 |
①补全条形统计图.
②如果体育中考按自选项目占 、长跑占 、掷实心球占 计算成绩(百分制),分别计算小红和小强的体育中考成绩.
为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在 吨范围内,并将调查结果制成了如下尚不完整的统计表:
月平均用水量(吨 |
3 |
4 |
5 |
6 |
7 |
频数(户数) |
4 |
|
9 |
10 |
7 |
频率 |
0.08 |
0.40 |
|
|
0.14 |
请根据统计表中提供的信息解答下列问题:
(1)填空: , , .
(2)这些家庭中月平均用水量数据的平均数是 ,众数是 ,中位数是 .
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
为了庆祝中国共产党建党100周年,某校开展了学党史知识竞赛.参加知识竞赛的学生分为甲乙两组,每组学生均为20名,赛后根据竞赛成绩得到尚不完整的统计图表(如图),已知竞赛成绩满分为100分,统计表中 , 满足 .请根据所给信息,解答下列问题:
甲组20名学生竞赛成绩统计表
成绩(分 |
70 |
80 |
90 |
100 |
人数 |
3 |
|
|
5 |
(1)求统计表中 , 的值;
(2)小明按以下方法计算甲组20名学生竞赛成绩的平均分是: (分 .根据所学统计知识判断小明的计算是否正确,若不正确,请写出正确的算式并计算出结果;
(3)如果依据平均成绩确定竞赛结果,那么竞赛成绩较好的是哪个组?请说明理由.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号