江苏省兴化市常青藤学校联盟八年级下学期第三次月度联考数学试卷
若方程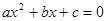
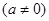 中,
中,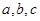 满足
满足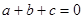 和
和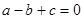 ,则方程的根( ).
,则方程的根( ).
| A.1,0 | B.-1,0 | C.1,-1 | D.无法确定 |
分式 (xyz≠0)中x,y,z的值都变为原来的2倍,则分式的值变为原来的( ).
(xyz≠0)中x,y,z的值都变为原来的2倍,则分式的值变为原来的( ).
| A.2倍 | B.4倍 | C.6倍 | D.8倍 |
某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为 ( ) .
| A.x(x+1)=1035 |
| B.x(x-1)=1035×2 |
| C.x(x-1)=1035 |
| D.2x(x+1)=1035 |
为了估计鱼池里有多少条鱼,先捕上100条作上记号,然后放回到鱼池里,过一段时间,待有记号的鱼完全混合鱼群后,再捕上200条鱼,发现其中带记号的鱼20条,则可判断鱼池里大约有____ ____条鱼.
如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则
∠A1OB= °.
货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意可列方程 .
若A(-1,y1)、B(-2,y2)是反比例函数y= (m为常数,m≠
(m为常数,m≠ )图象上的两点,且y1>y2,则m的取值范围是 .
)图象上的两点,且y1>y2,则m的取值范围是 .
如图,△AOB为等边三角形,点B的坐标为( 2,0),过点C(2,0)作直线
2,0),过点C(2,0)作直线 交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数的解析式为
交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数的解析式为 .
.
(本题8分)已知关于x的方程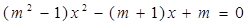 .
.
(1)m为何值时,此方程是一元一次方程?
(2)m满足什么条件时,此方程是一元二次方程?并写出一元二次方程的二次项系数、一次项系数及常数项(用含m的代数式表示).
(本题10分)根据题目条件,求代数式的值:
(1)已知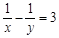 ,求
,求 的值.
的值.
(2)若x=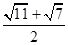 , y=
, y= ,求代数式x2-xy+y2的值.
,求代数式x2-xy+y2的值.
(本题10分)某楼盘准备以每平方米8000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米6480元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费是每平方米每月1.5元.请问哪种方案更优惠?
(本题10分)一学校为了绿化校园环境,向某园林公司购买了一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价为120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元.该校最终向园林公司支付树苗款8800元.请问该校共购买了多少棵树苗?
(本题10分)已知:关于x的方程kx2-(3k-1)x+2(k-1)=0,
(1)求证:无论k为何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且|x1-x2|=2,求k的值.
(本题12分)如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为t s(0<t<6),试尝试探究下列问题: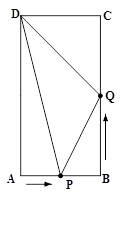
(1)当t为何值时,△PBQ的面积等于8cm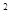 ?
?
(2)当t为何值时,△PBQ的面积最大,并求出这个最大面积;
(3)当t为何值时,△PDQ是等腰三角形?写出探索过程.

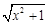
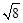
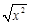
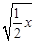
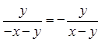
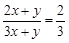
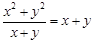

 与
与 是同类二次根式;
是同类二次根式; 有两个相等的实数根,则m= .
有两个相等的实数根,则m= . 的一个根为1,则另一个根为 .
的一个根为1,则另一个根为 . 的方程
的方程 的解是正数,则
的解是正数,则 的取值范围是 .
的取值范围是 . —
— —(
—( —
— );
);  .
.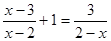 ;(2)
;(2)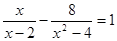 .
. (用配方法).
(用配方法).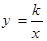 (x>0)上,点C在双曲线
(x>0)上,点C在双曲线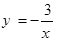 (x<0)上,点A是x轴上一动点,连接BC、AC、AB.
(x<0)上,点A是x轴上一动点,连接BC、AC、AB.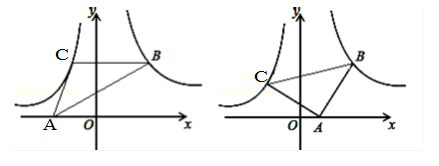
 粤公网安备 44130202000953号
粤公网安备 44130202000953号