湖北省武汉市黄陂区部分学校七年级5月联考数学试卷
在实数 ,0 ,
,0 , ,
, ,
,  中,无理数有( )
中,无理数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下列各点,在第二象限的点是( )
| A.(2,3) | B.(2,-3) | C.(-2,3) | D.(-2,-3) |
已知 是关于x、y的二元一次方程
是关于x、y的二元一次方程 的一个解,则m的值是( )
的一个解,则m的值是( )
| A.2 | B.-2 | C.1 | D.-1 |
甲、乙两仓库共存粮450吨,现从甲仓库运出存粮的60%,从乙仓库运出存粮的40%,结果乙仓库剩余的粮食比甲仓库剩余的粮食多30吨,若设甲仓库原来存粮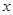 吨,乙仓库原来存粮
吨,乙仓库原来存粮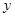 吨,则所列方程组正确的是( )
吨,则所列方程组正确的是( )
A.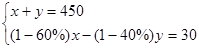 |
B.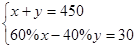 |
C.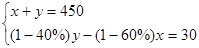 |
D.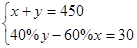 |
将一直角三角板与两边平行的纸条如图所示放置,若∠1=2∠2,则∠3的度数是( )
| A.100° | B.120° | C.130° | D.150° |
如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
| A.(9,12) | B.(9,9) | C.(9,6) | D.(9,3) |
一条进村公路修到湖边时需拐弯绕湖而过,如图,如果第一次拐弯∠A=100°,第二次拐弯∠B=160°,第三次拐弯的角是∠C,要使第三次拐弯后道路恰好与第一次拐弯之前道路平行,则∠C度数是( )
| A.110° | B.120° | C.135° | D.155° |
m为正整数,已知二元一次方程组 有整数解,则m2的值为( )
有整数解,则m2的值为( )
| A.4 | B.49 | C.4或49 | D.1或49 |
在平面直角系中,已知直线 与坐标轴交于A、B (0,-5)两点,且直线
与坐标轴交于A、B (0,-5)两点,且直线 与坐标轴围成的图形面积为 10,则点A的坐标为 .
与坐标轴围成的图形面积为 10,则点A的坐标为 .
如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是  .
.
购买铅笔7支,作业本3本,圆珠笔1支共需3元;购买铅笔10支,作业本4本,圆珠笔1
支共需4元,则购买铅笔11支、作业本5本圆珠笔2支共需 元。
如图,已知∠1,∠2互为补角,且∠3=∠B,求证:∠AFE=∠ACB.
证明:∵∠1+_______=180°,∠l+∠2=180°
∴_______=_______
∴DF∥AB
∴∠3=_______( )
又∵∠3=∠B
∴∠B=_______( )
∴EF∥CB
∴∠AFE=∠ACB( )
如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P( )经平移后对应点为P′(
)经平移后对应点为P′( )。
)。
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为 。
(本题10分)如图,∠1=∠2,∠BAE=∠BDE,EA平分∠BEF。
(1)求证:AB∥DE;
(2)BD平分∠EBC吗?为什么?
某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人,他们经过培训后上岗,也能独立进行进行电动汽车的安装。生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘 (0<
(0< <10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务(每月完成的量相同),那么工厂有哪几种新工人的招聘方案?
<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务(每月完成的量相同),那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
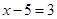


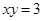
 ,则
,则 的值为( )
的值为( ) = ;
= ; = ;
= ; = .
= . 的
的 与7的差不小于3,用不等式表示为: .
与7的差不小于3,用不等式表示为: . 、
、 满足方程组
满足方程组 ,则
,则 的值为 .
的值为 .



 ,甲同学正确解得
,甲同学正确解得 ,而乙同学粗心,把
,而乙同学粗心,把 给看错了,解得
给看错了,解得 ,求
,求 的值。
的值。 ,
, )的横纵坐标满足条件:
)的横纵坐标满足条件: .
.
 轴于A,BC⊥
轴于A,BC⊥ 轴于C,P为CB延长线上一点,OP交BA于E,若
轴于C,P为CB延长线上一点,OP交BA于E,若 ,求P、E两点坐标。
,求P、E两点坐标。 粤公网安备 44130202000953号
粤公网安备 44130202000953号