江苏省扬州市邗江区九年级上学期期中测试数学试卷
已知△ABC∽△A1B1C1,且∠A=50°,∠B=95°,则∠C1等于( )
| A.50° | B.95° | C.35° | D.25° |
如图,△ABC内接于⊙O,∠A =60°,则∠BOC等于( )
| A.30° | B.120° | C.110° | D.100° |
已知⊙O的半径为5㎝,P到圆心O的距离为6㎝,则点P在⊙O( )
| A.外部 | B.内部 | C.圆上 | D.不能确定 |
△ABC与△A′B′C′相似,且△ABC与△A′B′C′的相似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )
| A.3 | B.6 | C.9 | D.12 |
如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
| A.3:2 | B.3:1 | C.1:1 | D.1:2 |
若非零实数 满足
满足 ,则关于x的一元二次方程
,则关于x的一元二次方程 一有一个根为( )
一有一个根为( )
| A.3 | B.-3 | C.0 | D.无法确定 |
如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
A.( ,3)、(﹣
,3)、(﹣ ,4)
,4)
B.( ,3)、(﹣
,3)、(﹣ ,4)
,4)
C.( ,
, )、(﹣
)、(﹣ ,4)
,4)
D.( ,
, )、(﹣
)、(﹣ ,4)
,4)
在比例尺为1∶5 000 000的地图上,量得甲、乙两地的距离是15cm,则两地的实际距离是 km.
如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为 .
如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=70°,连接AE,则∠AEB的度数为 .
已知,如图弧BC比弧AD的度数多20°,弦AB与CD交于点E,∠CEB=60°,则∠CAB= °.
如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是 cm
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC向上平移3个单位得到△A1B1C1,请画出△A1B1C1;
(2)请画一个格点△A2B2C2,使△A2B2C2∽△ABC,且相似比不为1.
已知关于 的方程
的方程 ,
,
(1)若该方程的一个根为1,求 的值及该方程的另一根;
的值及该方程的另一根;
(2)求证:不论 取何实数,该方程都有两个不相等的实数根.
取何实数,该方程都有两个不相等的实数根.
如图所示,在△ABC中,AB=BC=12 cm,∠ABC=80°,BD是∠ABC的平分线,DE∥BC.
(1)求∠EDB的度数;
(2)求DE的长.
阅读下面的例题:解方程 的过程如下:
的过程如下:
(1)当 时,原方程化为
时,原方程化为 ,解得:
,解得: ,
, (不合题意,舍去).
(不合题意,舍去).
(2)当 时,原方程可化为
时,原方程可化为 ,解得:
,解得: ,
, (不合题意,舍去).所以,原方程的解是:
(不合题意,舍去).所以,原方程的解是: ,
, .请参照例题
.请参照例题
解方程:
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
已知关于 的一元二次方程
的一元二次方程 ,其中a、b、c分别为△ABC三边的长.
,其中a、b、c分别为△ABC三边的长.
(1)如果 是方程的根,试判断△ABC的形状,并说明理由;
是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
已知:如图等边△ABC内接于⊙O,点P是劣弧BC上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由.
(2)若AP不过圆心O,如图②,请你判断△PDC是什么三角形?并说明理由.
 是方程
是方程 的两个根,则
的两个根,则 的值为( )
的值为( )

 的解是 .
的解是 .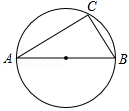
 化为
化为 ,则
,则 = .
= . 的解是
的解是 ,则
,则 的值是 .
的值是 . 的方程
的方程 有两个实数根,那么
有两个实数根,那么 的取值范围是 .
的取值范围是 .

 、
、 是方程
是方程 的两实数根,求
的两实数根,求 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号