安徽省芜湖县六校九年级上学期第一次联考数学试卷
若点(2,5),(4,5)在抛物线y=ax2+bx+c上,则它的对称轴是( ).
A.x= |
B.x=1 | C.x=2 | D.x=3 |
已知一元二次方程 有两个不相等的实数根,则k的范围是( )
有两个不相等的实数根,则k的范围是( )
A.k> |
B.k< |
C.k≤ 且k≠0 且k≠0 |
D.k< 且k≠0 且k≠0 |
若关于 的一元二次方程
的一元二次方程 的两根分别为
的两根分别为 ,
, ,则p、q的值分别是( )
,则p、q的值分别是( )
| A.3、2 | B.-2、3 | C.-3、2 | D.2、3 |
有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中,平均一个人传染的人数为( ).
| A.8人 | B.9人 | C.10人 | D.11人 |
若函数y=mx2+(m+2)x 的图像与x轴只有一个交点,那么m的值为( )
| A.—2 | B.0或2 | C.2或—2 | D.0或—2 |
如果三角形的两边长分别是方程x2﹣8x+15=0的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是( )
| A.5.5 | B.5 | C.4.5 | D.4 |
已知二次函数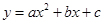 (
( <0)的图象如图所示,当
<0)的图象如图所示,当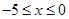 时,下列说法正确的是( )
时,下列说法正确的是( )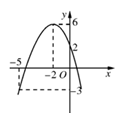
| A.有最小值-5、最大值0 |
| B.有最小值-3、最大值6 |
| C.有最小值0、最大值6 |
| D.有最小值2、最大值6 |
已知 ,点A (a,y1 ),B( a+1,y2)都在 二次函数
,点A (a,y1 ),B( a+1,y2)都在 二次函数 图像上,那么y1 、y2的大小关系是 .
图像上,那么y1 、y2的大小关系是 .
抛物线y=-2x2向左平移1个单位,再向上平移7个单位得到的抛物线的解析式是____________.
已知二次函数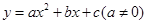 的图象如图所示,则下列结论:
的图象如图所示,则下列结论: ;
;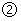 方程
方程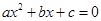 的两根之和大于0;③2a+b<0;④
的两根之和大于0;③2a+b<0;④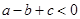 ,其中正确的是 (填序号)
,其中正确的是 (填序号) 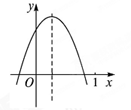
已知关于x的一元二次方程x2+2(k-1)x+k2-1=0有两个不相等的实数根.
(1)、求实数k的取值范围;
(2)、0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.
如图,抛物线 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题: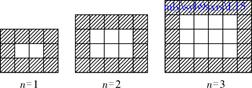
…
(1)在第n个图中,每一横行共有________块瓷砖,每一竖列共有________块瓷砖;(均用含n的代数式表示)
(2)设铺设地面所用瓷砖的总块数为y,请写出y与n的函数关系式;(不要求写出自变量n的取值范围)
(3)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
(4)若黑色瓷砖每块4元,白色瓷砖每块3元,则购买506块瓷砖共需花费多少元?
(5)是否存在黑色瓷砖与白色瓷砖的块数相等的情形?请通过计算说明理由.
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。
求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多
如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,△MON的面积为 ?
?
行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
| 刹车时车速/km·h-1 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
| 刹车距离/m |
0 |
0.3 |
1.0 |
2.1 |
3.6 |
5.5 |
7.8 |
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象.估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?
 的二次项系数、一次项系数、常数项分别是( )
的二次项系数、一次项系数、常数项分别是( )



 左边变成完全平方式后,方程是( )
左边变成完全平方式后,方程是( )



 与二次函数
与二次函数 的图像可能是( )
的图像可能是( )
 是方程
是方程 的一个根,求
的一个根,求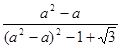 的值
的值 粤公网安备 44130202000953号
粤公网安备 44130202000953号