如图所示,滑雪道 由坡道和水平道组成,且平滑连接,坡道倾角均为 。平台 与缓冲坡 相连,若滑雪者从 点由静止开始下滑,恰好到达 点。滑雪者现从 点由静止开始下滑,从 点飞出。已知 、 间的距离为 ,滑雪者与滑道间的动摩擦因数均为 ,重力加速度为 ,不计空气阻力。
(1)求滑雪者运动到 点的时间 ;
(2)求滑雪者从 点飞出的速度大小 ;
(3)若滑雪者能着陆在缓冲坡 上,求平台 的最大长度 。
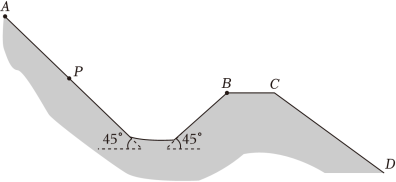
如图所示,滑雪道 由坡道和水平道组成,且平滑连接,坡道倾角均为 。平台 与缓冲坡 相连,若滑雪者从 点由静止开始下滑,恰好到达 点。滑雪者现从 点由静止开始下滑,从 点飞出。已知 、 间的距离为 ,滑雪者与滑道间的动摩擦因数均为 ,重力加速度为 ,不计空气阻力。
(1)求滑雪者运动到 点的时间 ;
(2)求滑雪者从 点飞出的速度大小 ;
(3)若滑雪者能着陆在缓冲坡 上,求平台 的最大长度 。
