如图所示，P、Q两平行金属板间存在着平行于纸面的匀强电场和垂直纸面向外的匀强磁场，两板间的距离为d，电势差为U；金属板下方存在一有水平边界、方向垂直纸面向外的匀强磁场，磁感应强度为B。电荷量为q的带正电的粒子，以速度v垂直于电场和磁场匀速通过P、Q两金属板间，并沿垂直磁场方向进入金属板下方的磁场，做半径为R的匀速圆周运动。不计两极板电场的边缘效应及粒子所受的重力。求：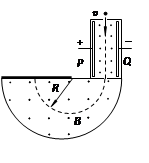
（1）P、Q两金属板间匀强电场场强E的大小；
（2）P、Q两金属板间匀强磁场磁感应强度B0的大小；
（3）粒子的质量m。
如图所示，一条长为L的绝缘细线，上端固定，下端系一质量为m的带电小球，将它置于电场强度为E、方向水平向右的匀强电场中，当小球平衡时，悬线与竖直方向的夹角为45°．
（1）小球带何种电荷？电荷量为多少？
（2）若将小球向左拉至悬线成水平位置，然后由静止释放小球，则放手后小球做什么运动？经多长时间到达最低点．
质点从静止开始做匀加速直线运动，经4s后速度达到20m/s，然后匀速运动了10s，接着经5s匀减速运动后静止。求：
（1）质点在加速运动阶段和减速阶段的加速度的大小？
（2）质点在整个过程的平均速度是多大？
如图所示，在场强为E的匀强电场中，一绝缘轻质细杆L可绕O点在竖直平面内自由转动，A端有一个带正电的小球，电荷量为q，质量为m。将细杆从水平位置自由释放，则：
（1）请说明小球由A到B的过程中电势能如何变化?
（2）求出小球在最低点时的速率
（3）求在最低点时绝缘杆对小球的作用力.
公路上行驶的两汽车之间应保持一定的安全距离．当前车突然停止时，后车司机可以采取刹车措施，使汽车在安全距离内停下而不会与前车相碰．通常情况下，人的反应时间和汽车系统的反应时间之和为1 s，当汽车在晴天干燥沥青路面上以108 km/h的速度匀速行驶时，安全距离为120 m．设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的
，若要求安全距离仍为120 m，求汽车在雨天安全行驶的最大速度．
粤公网安备 44130202000953号