如图所示为圆柱形区域的横截面，在没有磁场的情况下，带电粒子（不计重力）以某一初速度沿截面直径方向入射，穿过此区域的时间为t ，在该区域加沿轴线垂直纸面向外方向的匀磁强场，磁感应强度大小为B，带电粒子仍以同一初速度沿截面直径入射并沿某一直径方向飞出此区域时，速度方向偏转角为600，如图所示。根据上述条件可求下列哪几个物理量 （ ）
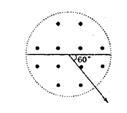
① 带电粒子的比荷 ② 带电粒子在磁场中运动的周期
③ 带电粒子在磁场中运动的半径 ④ 带电粒子的初速度
| A．①② | B．①③ | C．②③ | D．③④ |
如图所示，轻质弹簧的劲度系数为20N/cm，用其拉着一个重200N的物体在水平面上运动．当弹簧的伸长量为4cm时，物体恰在水平面上做匀速直线运动．
（1）求物体与水平面间的动摩擦因数；
（2）当弹簧的伸长量为6cm时，物体受到的水平拉力有多大？这时物体受到的摩擦力有多大？
（3）如果在物体运动的过程中突然撤去弹簧，而物体在水平面上能继续滑行，这时物体受到的摩擦力有多大？
一列从车站开出的火车，在平直轨道上做匀加速直线运动，已知这列火车的长度为L，火车头经过某路标时的速度为v1，而车尾经过此路标时的速度为v2，求：
（1）火车的加速度a．
（2）火车中点经过此路标时的速度v．
（3）整列火车通过此路标所用的时间t．
汽车以10m/s的速度在平直公路上匀速行驶，刹车后经2s速度变为6m/s，求：
（1）刹车过程中的加速度及刹车4s后的速度？
（2）刹车后8s内前进的距离
（3）停止运动前2s内的位移．
如图所示，放在水平面上质量为m的物体受一个斜上的拉力F，这个力与水平方向成θ角，在此力作用下，物体水平向右匀速滑动，求：
（1）物体与水平面间的动摩擦因数μ．
（2）如果把此力F撤去，此时物体做什么运动？摩擦力多大？
（3）如果在本题中已知动摩擦因数μ，现只给物体施加一个与水平方向成θ角的斜向下的推力F′，物体仍能保持匀速运动，求F′多大？
粤公网安备 44130202000953号