如图（a）所示，一倾角为37°的传送带以恒定速度运行．现将一质量m=2kg的小物体以某一初速度放上传送带，物体相对地面的速度随时间变化的关系如图（b）所示，取沿传送带向上为正方向，g=10m/s2，sin37°=0.6，cos37°=0.8．求：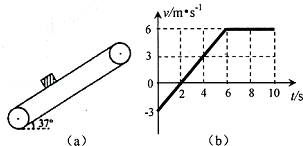
（1）0﹣10s内物体位移的大小；
（2）物体与传送带间的动摩擦因数；
（3）0﹣10s内物体机械能增量及因与传送带摩擦产生的热量Q．
如图，某一新型发电装置的发电管是横截面为矩形的水平管道，管道的长为、宽度为
、高为
，上下两面是绝缘板，前后两侧面
、
是电阻可忽略的导体板，两导体板与开关S和定值电阻
相连。整个管道置于磁感应强度大小为
，方向沿
轴正方向的匀强磁场中。管道内始终充满电阻率为
的导电液体（有大量的正、负离子），且开关闭合前后，液体在管道进、出口两端压强差的作用下，均以恒定速率v0沿x轴正向流动，液体所受的摩擦阻力不变。
（1）求开关闭合前，、
两板间的电势差大小
；
（2）求开关闭合前后，管道两端压强差的变化；
（3）调整矩形管道的宽和高，但保持其它量和矩形管道的横截面不变，求电阻
可获得的最大功率
及相应的宽高比
的值。
图为某游乐场内水上滑梯轨道示意图，整个轨道在同一竖直平面内，表面粗糙的段与四分之一光滑圆弧轨道
在
点水平相切。点
距水面的高度为H，圆弧轨道BC的半径为R，圆心
恰在水面。一质量为
的游客（视为质点）可从轨道
的任意位置滑下，不计空气阻力。
（1）若游客从点由静止开始滑下，到
点时沿切线方向滑离轨道落在水面
点，
，求游客滑到的速度
大小及运动过程轨道摩擦力对其所做的功
；
（2）若游客从段某处滑下，恰好停在
点，有因为受到微小扰动，继续沿圆弧轨道滑到
点后滑离轨道，求
点离水面的高度
。（提示：在圆周运动过程中任一点，质点所受的向心力与其速率的关系为
)
如图，真空中xOy平面直角坐标系上的三点构成等边三角形，边长
。若将电荷量均为
的两点电荷分别固定在
、
点，已知静电力常量
。求：
（1）两点电荷间的库仑力大小；
（2）点的电场强度的大小和方向。
已知地球的自转周期和半径分别为和
，地球同步卫星
的圆轨道半径为
。卫星B沿半径为
的圆轨道在地球赤道的正上方运行，其运行方向与地球自转方向相同。求：
（1）卫星做圆周运动的周期；
（2）卫星和
连续地不能直接通讯的最长时间间隔（信号传输时间可忽略）。
粤公网安备 44130202000953号