如图所示，一个不计厚度上表面光滑的电动平板长L=3.75m，平板上左侧有一挡板，紧靠挡板处有一可看成质点的小球．开始时，平板与小球一起在水平面上向右做匀速运动，速度大小为v0=5m/s．某时刻平板开始制动，加速度大小a1=4m/s2．经过一段时间，小球从平板右端滑出并滑落到地面上接着在地面上做匀减速直线运动，运动t2=2.5s停下．求：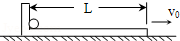
（1）小球在地面上做匀减速直线运动的加速度a2大小
（2）从开始制动到小球离开平板所用的时间t1
（3）最终小球离平板右端的距离s
如图所示，质量M＝8 kg的小车放在光滑的水平面上，在小车左端加一水平推力F＝8 N，当小车向右运动的速度达到1.5 m/s时，在小车前端轻轻地放上一个大小不计，质量为m＝2 kg的小物块，小物块与小车间的动摩擦因数μ＝0.2，当二者达到相同速度时，物块恰好滑到小车的最左端。取g＝10 m/s2。则：
(1)小物块放上后，小物块及小车的加速度各为多大？
(2)小车的长度L是多少？
如图所示，质量为m1＝5 kg的滑块，置于一粗糙的斜面上，用一平行于斜面的大小为30 N的力F推滑块，滑块沿斜面向上匀速运动，斜面体质量m2＝10 kg，且始终静止，取g＝10 m/s2，求：
(1)斜面对滑块的摩擦力；
(2)地面对斜面体的摩擦力和支持力。
如图所示，一质量为
，长为
的木板放在水平地面上，已知木板与地面间的动摩擦因数为
，在此木板的右端上还有一质量为
的小物块，且视小物块为质点，木板厚度不计.今对木板突然施加一个
的水平向右的拉力，
.
（1）若木板上表面光滑，则小物块经多长时间将离开木板？
（2）若小物块与木板间的动摩擦因数为
、小物块与地面间的动摩擦因数为
，小物块相对木板滑动且对地面的总位移
，求值.
一小物块随足够长的水平传送带一起运动，被一水平向左飞的子弹击中并从物块中穿过，如图1所示.固定在传送带右端的位移传感器纪录了小物块被击中后的位移
随时间
的变化关系如图2所示（图象前3s内为二次函数，3～4.5s内为一次函数，取向左运动的方向为正方向）. 已知传送带的速度
保持不变，
取
.
（1）求传送带速度的大小；
（2）求0时刻物块速度
的大小；
（3）画出物块对应的
图象。
的斜面上放一木板
，重为
，板上放一重为
的木箱
，斜面上有一固定的挡板，先用平行于斜面的绳子把木箱与挡板拉紧，然后在木板上施加一平行斜面方向的拉力
，使木板从木箱下匀速抽出，此时，绳子的拉力
. 设木板与斜面间的动摩擦因数
，求拉力
粤公网安备 44130202000953号