如图所示，光滑水平轨道右边与墙壁连接，木块A、B和半径为0.5m的1/4光滑圆轨道C静置于光滑水平轨道上，A、B、C质量分别为1.5kg、0.5kg、4kg。现让A以6m/s的速度水平向右运动，之后与墙壁碰撞，碰撞时间为0.3s，碰后速度大小变为4m/s。当A与B碰撞后会立即粘在一起运动，已知g=10m/s2，求：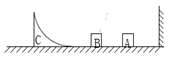
①A与墙壁碰撞过程中，墙壁对小球平均作用力的大小；
②AB第一次滑上圆轨道所能到达的最大高度h。
如图所示，在坐标系xOy中，y轴右侧有一匀强电场；在第二、三象限内有一有界匀强磁场，其上、下边界无限远，右边界为y轴、左边界为平行于y轴的虚线，磁场的磁感应强度大小为B，方向垂直纸面向里。一带正电，电量为q、质量为m的粒子以某一速度自磁场左边界上的A点射入磁场区域，并从O点射出，粒子射出磁场的速度方向与x轴的夹角θ＝45°，大小为v．粒子在磁场中的运动轨迹为纸面内的一段圆弧，且弧的半径为磁场左右边界间距的
倍。粒子进入电场后，在电场力的作用下又由O点返回磁场区域，经过一段时间后再次离开磁场。已知粒子从A点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。忽略重力的影响。求：
（1）粒子经过A点时速度的方向和A点到x轴的距离；
（2）匀强电场的大小和方向；
（3）粒子从第二次离开磁场到再次到达磁场所用的时间。
如图甲所示，一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L＝1.0 m，NQ两端连接阻值R＝1.0 Ω的电阻，磁感应强度为B的匀强磁场垂直于导轨所在平面向上，导轨平面与水平面间的夹角θ＝300。一质量m="0.20" kg，阻值r="0.50" Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M="0.60" kg的重物相连。细线与金属导轨平行。金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示，已知金属棒在0～0.3 s内通过的电量是0.3～0.6 s内通过电量的
，g="10" m/s2，求：
（1）0～0.3 s内棒通过的位移；
（2）金属棒在0～0.6 s内产生的热量。
如图所示，水平地面上放置一个质量为m的物体，在与水平方向成θ角、斜向右上方的拉力F的作用下沿水平地面运动。物体与地面间的动摩擦因数为μ，重力加速度为g。求：
（1）若物体在拉力F的作用下能始终沿水平面向右运动，拉力F的大小范围；
（2）已知m＝10 kg、μ＝0.5，g＝10 m/s2，若物体以恒定加速度a＝5 m/s2向右做匀加速直线运动，维持这一加速度的拉力F的最小值。
如图，光滑水平面上有三个物块A、B和C，它们具有相同的质量，且位于同一直线上。开始时，三个物块均静止，先让A以一定速度与B碰撞，碰后它们粘在一起，然后又一起与C碰撞并粘在一起，求前后两次碰撞中系统损失的动能之比。 
的木板，倾斜放置，倾角为45°，现有一弹性小球，从与木板上端等高的某处自由释放，小球落到木板上反弹时，速度大小不变，碰撞前后，速度方向与木板的夹角相等，欲使小球一次碰撞后恰好落到木板下端，则小球释放点距木板上端的水平距离为___________。
粤公网安备 44130202000953号