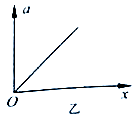
如图甲所示,质量分别为2m和m的A.B两物体通过足够长的细线绕过光滑轻质滑轮,轻弹簧下端与地面相连,B放在弹簧上端但不栓接,A放在光滑的固定斜面上,开始时用手按住A,使细线刚好拉直且无拉力,滑轮左侧细线竖直,右侧细线与斜面平行,释放A后它沿斜面下滑,物体B在弹簧恢复原长之前的加速度随弹簧压缩量x的变化规律如图乙所示,当弹簧刚好恢复原长时,B获得的速度为v,若重力加速度为g,求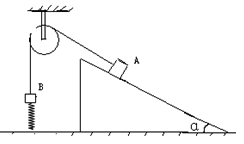
(1)斜面倾角α
(2)A和B刚开始运动时,细线中的张力
(3)弹簧最大的弹性势能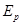
如图甲所示,质量分别为2m和m的A.B两物体通过足够长的细线绕过光滑轻质滑轮,轻弹簧下端与地面相连,B放在弹簧上端但不栓接,A放在光滑的固定斜面上,开始时用手按住A,使细线刚好拉直且无拉力,滑轮左侧细线竖直,右侧细线与斜面平行,释放A后它沿斜面下滑,物体B在弹簧恢复原长之前的加速度随弹簧压缩量x的变化规律如图乙所示,当弹簧刚好恢复原长时,B获得的速度为v,若重力加速度为g,求

(1)斜面倾角α
(2)A和B刚开始运动时,细线中的张力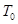
(3)弹簧最大的弹性势能