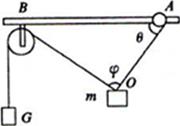
如图所示,细绳OA的O端与质量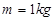 的重物相连,A端与轻质圆环(重力不计)相连,圆环套在水平棒上可以滑动;定滑轮固定在B处,跨过定滑轮的细绳,两端分别与重物m、重物G相连,若两条细绳间的夹角
的重物相连,A端与轻质圆环(重力不计)相连,圆环套在水平棒上可以滑动;定滑轮固定在B处,跨过定滑轮的细绳,两端分别与重物m、重物G相连,若两条细绳间的夹角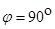 ,OA与水平杆的夹角
,OA与水平杆的夹角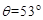 圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,滑动摩擦力等于最大静摩擦力.(已知
圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,滑动摩擦力等于最大静摩擦力.(已知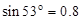 ;
;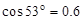 ):
):
(1)圆环与棒间的动摩擦因数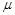 ;
;
(2)重物G的质量M
如图所示,细绳OA的O端与质量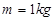 的重物相连,A端与轻质圆环(重力不计)相连,圆环套在水平棒上可以滑动;定滑轮固定在B处,跨过定滑轮的细绳,两端分别与重物m、重物G相连,若两条细绳间的夹角
的重物相连,A端与轻质圆环(重力不计)相连,圆环套在水平棒上可以滑动;定滑轮固定在B处,跨过定滑轮的细绳,两端分别与重物m、重物G相连,若两条细绳间的夹角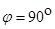 ,OA与水平杆的夹角
,OA与水平杆的夹角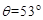 圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,滑动摩擦力等于最大静摩擦力.(已知
圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,滑动摩擦力等于最大静摩擦力.(已知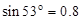 ;
;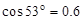 ):
):
(1)圆环与棒间的动摩擦因数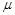 ;
;
(2)重物G的质量M