某同学在某砖墙前的高处水平抛出一石子,石子在空中运动的部分轨迹照片如图所示。从照片可看出石子恰好垂直打在一倾角为37°的斜坡上的A点。已知每块砖的平均厚度为20 cm,抛出点到A点竖直方向刚好相距100块砖,求: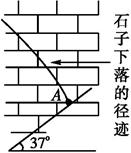
(1)石子在空中运动的时间t;
(2)石子水平抛出的速度v0。
相关试题
特技演员从高80m的大楼楼顶自由下落，在演员开始下落的同时汽车从60m远处由静止向楼底先匀加速运动t0 =3s，再匀速行驶到楼底，演员刚好能落到汽车上（不计空气阻力，人和汽车看作质点，g取10m/s2），求:
（1）汽车开到楼底的时间t；
（2）汽车匀加速运动时的加速度a和汽车匀速行驶的速度v
质量为
的物体放在光滑水平地面上，在水平方向的恒定拉力
的作用下，从静止开始做匀加速运动。在前4s内滑行了8m的距离，取
。求：
（1）4s内拉力对物体所做的功。
（2）物体在4s末的动能。
核聚变能是一种具有经济性能优越、安全可靠、无环境污染等优势的新能源。近年来，受控核聚变的科学可行性已得到验证，目前正在突破关键技术，最终将建成商用核聚变电站。一种常见的核聚变反应是由氢的同位素氘（又叫重氢）和氚（又叫超重氢）聚合成氦，并释放一个中子。若已知氘原子的质量为2.0141u，氚原子的质量为3.0160u，氦原子的质量为4.0026u，中子的质量为1.0087u，1u＝1.66×10-27kg。
（1）写出氘和氚聚合的反应方程。
（2）试计算这个核反应释放出来的能量。
（3）若建一座功率为3.0×105kw的核聚变电站，假设聚变所产生的能量有一半变成了电能，每年要消耗多少氘的质量？（一年按3.2×107s计算，光速c＝3.00×108m/s，结果取二位有效数字）
粤公网安备 44130202000953号