边长为L=0.2m的正方形区域内有垂直纸面向里的匀强磁场,穿过该区域磁场的磁感应强度随时间变化的图象如图乙所示,将边长为 ,匝数n=100,线圈电阻r=1.0Ω的正方形线圈abcd放入磁场,线圈所在平面与磁感线垂直,如图甲所示.求:
,匝数n=100,线圈电阻r=1.0Ω的正方形线圈abcd放入磁场,线圈所在平面与磁感线垂直,如图甲所示.求: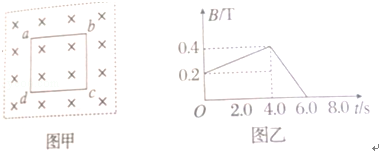
(1)回路中感应电流的方向及磁感应强度的变化率 ;
;
(2)在0~4.0s内通过线圈的电荷量q;
(3)0~6.0s内整个闭合电路中产生的热量.
边长为L=0.2m的正方形区域内有垂直纸面向里的匀强磁场,穿过该区域磁场的磁感应强度随时间变化的图象如图乙所示,将边长为 ,匝数n=100,线圈电阻r=1.0Ω的正方形线圈abcd放入磁场,线圈所在平面与磁感线垂直,如图甲所示.求:
,匝数n=100,线圈电阻r=1.0Ω的正方形线圈abcd放入磁场,线圈所在平面与磁感线垂直,如图甲所示.求:
(1)回路中感应电流的方向及磁感应强度的变化率 ;
;
(2)在0~4.0s内通过线圈的电荷量q;
(3)0~6.0s内整个闭合电路中产生的热量.