如图所示的凹形场地,两端是半径为L=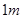 的光滑1/4圆弧面,中间长为2L的粗糙水平面.质量为3m的滑块乙开始停在水平面的中点O处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内与乙发生碰撞,碰后甲以碰前一半的速度反弹.已知甲、乙与水平面的动摩擦因数分别为μ1=0.2、μ2=0.1,甲、乙的体积大小忽略不计.g=10 m/s2.求:
的光滑1/4圆弧面,中间长为2L的粗糙水平面.质量为3m的滑块乙开始停在水平面的中点O处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内与乙发生碰撞,碰后甲以碰前一半的速度反弹.已知甲、乙与水平面的动摩擦因数分别为μ1=0.2、μ2=0.1,甲、乙的体积大小忽略不计.g=10 m/s2.求:
(1)甲与乙碰撞前的速度.
(2)碰后瞬间乙的速度.
(3)甲、乙在O处发生碰撞后,请判断能否发生第二次碰撞?并通过计算确定甲、乙最后停止所在的位置.
如图所示的凹形场地,两端是半径为L=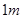 的光滑1/4圆弧面,中间长为2L的粗糙水平面.质量为3m的滑块乙开始停在水平面的中点O处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内与乙发生碰撞,碰后甲以碰前一半的速度反弹.已知甲、乙与水平面的动摩擦因数分别为μ1=0.2、μ2=0.1,甲、乙的体积大小忽略不计.g=10 m/s2.求:
的光滑1/4圆弧面,中间长为2L的粗糙水平面.质量为3m的滑块乙开始停在水平面的中点O处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内与乙发生碰撞,碰后甲以碰前一半的速度反弹.已知甲、乙与水平面的动摩擦因数分别为μ1=0.2、μ2=0.1,甲、乙的体积大小忽略不计.g=10 m/s2.求:
(1)甲与乙碰撞前的速度.
(2)碰后瞬间乙的速度.
(3)甲、乙在O处发生碰撞后,请判断能否发生第二次碰撞?并通过计算确定甲、乙最后停止所在的位置.