如图,一固定的竖直气缸有一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为,横截面积为,小活塞的质量为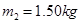 ,横截面积为;两活塞用刚性轻杆连接,间距保持为,气缸外大气压强为,温度为。初始时大活塞与大圆筒底部相距,两活塞间封闭气体的温度为,现气缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与气缸壁之间的摩擦,重力加速度取,求
,横截面积为;两活塞用刚性轻杆连接,间距保持为,气缸外大气压强为,温度为。初始时大活塞与大圆筒底部相距,两活塞间封闭气体的温度为,现气缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与气缸壁之间的摩擦,重力加速度取,求

(1)在大活塞与大圆筒底部接触前的瞬间,缸内封闭气体的温度;
(2)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强。
如图,一固定的竖直气缸有一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为,横截面积为,小活塞的质量为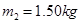 ,横截面积为;两活塞用刚性轻杆连接,间距保持为,气缸外大气压强为,温度为。初始时大活塞与大圆筒底部相距,两活塞间封闭气体的温度为,现气缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与气缸壁之间的摩擦,重力加速度取,求
,横截面积为;两活塞用刚性轻杆连接,间距保持为,气缸外大气压强为,温度为。初始时大活塞与大圆筒底部相距,两活塞间封闭气体的温度为,现气缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与气缸壁之间的摩擦,重力加速度取,求

(1)在大活塞与大圆筒底部接触前的瞬间,缸内封闭气体的温度;
(2)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强。