如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示.有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,求在0~4s时间内电阻R上产生的焦耳热.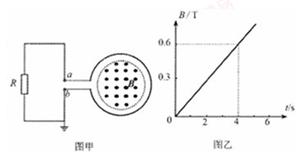
如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示.有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,求在0~4s时间内电阻R上产生的焦耳热.