如图a所示的平面坐标系xOy,在整个区域内充满了匀强磁场,磁场方向垂直坐标平面,磁感应强度B随时间变化的关系如图b所示。开始时刻,磁场方向垂直纸面向内(如图),t=0时刻有一带正电的粒子(不计重力)从坐标原点O沿x轴正向进入磁场,初速度为v0=2×103m/s。已知带电粒子的比荷为 ,其它有关数据见图中标示。试求:
,其它有关数据见图中标示。试求: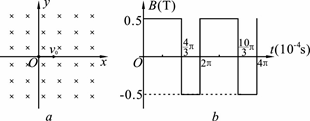
(1)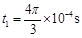 时粒子所处位置的坐标(x1,y1);
时粒子所处位置的坐标(x1,y1);
(2)带电粒子进入磁场运动后第一次到达y轴时离出发点的距离h;
(3)带电粒子是否还可以返回原点?如果可以,求返回原点经历的时间t′。
如图a所示的平面坐标系xOy,在整个区域内充满了匀强磁场,磁场方向垂直坐标平面,磁感应强度B随时间变化的关系如图b所示。开始时刻,磁场方向垂直纸面向内(如图),t=0时刻有一带正电的粒子(不计重力)从坐标原点O沿x轴正向进入磁场,初速度为v0=2×103m/s。已知带电粒子的比荷为 ,其它有关数据见图中标示。试求:
,其它有关数据见图中标示。试求:
(1)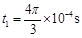 时粒子所处位置的坐标(x1,y1);
时粒子所处位置的坐标(x1,y1);
(2)带电粒子进入磁场运动后第一次到达y轴时离出发点的距离h;
(3)带电粒子是否还可以返回原点?如果可以,求返回原点经历的时间t′。