如图,质量m为5kg的物块(看作质点)在外力F1和F2的作用下正沿某一水平面向右做匀速直线运动。已知F1大小为50N,方向斜向右上方,与水平面夹角 ,F2大小为30N,方向水平向左,物块的速度
,F2大小为30N,方向水平向左,物块的速度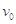 大小为11m/s.当物体运动到距初始位置距离
大小为11m/s.当物体运动到距初始位置距离 时,撤掉F1,
时,撤掉F1,
(1)求物块与水平地面之间的动摩擦因数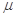 ;
;
(2)求撤掉F1以后,物块在6S末距初始位置的距离。
如图,质量m为5kg的物块(看作质点)在外力F1和F2的作用下正沿某一水平面向右做匀速直线运动。已知F1大小为50N,方向斜向右上方,与水平面夹角 ,F2大小为30N,方向水平向左,物块的速度
,F2大小为30N,方向水平向左,物块的速度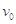 大小为11m/s.当物体运动到距初始位置距离
大小为11m/s.当物体运动到距初始位置距离 时,撤掉F1,
时,撤掉F1,
(1)求物块与水平地面之间的动摩擦因数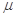 ;
;
(2)求撤掉F1以后,物块在6S末距初始位置的距离。