已知某星球半径为R,若宇航员随登陆舱登陆该星球后,在此星球表面某处以速度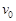 竖直向上抛出一个小球,小球能上升的最大高度为H,则(不考虑地球自转的影响)。
竖直向上抛出一个小球,小球能上升的最大高度为H,则(不考虑地球自转的影响)。
(1)此星球表面的重力加速度
(2)试根据以上条件推导第一宇宙速度v1的表达式;
(3)若在登陆前,宇宙飞船绕该星球做匀速圆周运动,运行轨道距离星球表面高度为h,求卫星的运行周期T。
已知某星球半径为R,若宇航员随登陆舱登陆该星球后,在此星球表面某处以速度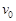 竖直向上抛出一个小球,小球能上升的最大高度为H,则(不考虑地球自转的影响)。
竖直向上抛出一个小球,小球能上升的最大高度为H,则(不考虑地球自转的影响)。
(1)此星球表面的重力加速度
(2)试根据以上条件推导第一宇宙速度v1的表达式;
(3)若在登陆前,宇宙飞船绕该星球做匀速圆周运动,运行轨道距离星球表面高度为h,求卫星的运行周期T。