质量 的空箱子静止在光滑水平面上,箱子内部有一个
的空箱子静止在光滑水平面上,箱子内部有一个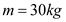 的金属块,不计金属块和箱子之间的摩擦,且箱子左侧壁到金属块距离为
的金属块,不计金属块和箱子之间的摩擦,且箱子左侧壁到金属块距离为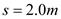 ,但是金属块一旦与箱子左侧壁接触后就不会分开。现在用水平向右的恒力
,但是金属块一旦与箱子左侧壁接触后就不会分开。现在用水平向右的恒力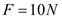 推箱子,
推箱子,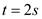 时撤去恒力,则
时撤去恒力,则
(i)恒力撤去前,金属块是否和箱子左侧壁发生碰撞?
(ii)金属块和箱子共同运动的速度是多大?
质量 的空箱子静止在光滑水平面上,箱子内部有一个
的空箱子静止在光滑水平面上,箱子内部有一个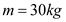 的金属块,不计金属块和箱子之间的摩擦,且箱子左侧壁到金属块距离为
的金属块,不计金属块和箱子之间的摩擦,且箱子左侧壁到金属块距离为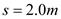 ,但是金属块一旦与箱子左侧壁接触后就不会分开。现在用水平向右的恒力
,但是金属块一旦与箱子左侧壁接触后就不会分开。现在用水平向右的恒力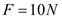 推箱子,
推箱子,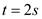 时撤去恒力,则
时撤去恒力,则
(i)恒力撤去前,金属块是否和箱子左侧壁发生碰撞?
(ii)金属块和箱子共同运动的速度是多大?