)质量为M="6" kg的木板B静止于光滑水平面上,物块A质量为6 kg,停在B的左端。质量为1 kg的小球用长为0. 8 m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2 m,物块与小球可视为质点,不计空气阻力。已知A、B间的动摩擦因数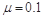 ,为使A、B达到共同速度前A不滑离木板,木板至少多长?
,为使A、B达到共同速度前A不滑离木板,木板至少多长?
)质量为M="6" kg的木板B静止于光滑水平面上,物块A质量为6 kg,停在B的左端。质量为1 kg的小球用长为0. 8 m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2 m,物块与小球可视为质点,不计空气阻力。已知A、B间的动摩擦因数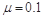 ,为使A、B达到共同速度前A不滑离木板,木板至少多长?
,为使A、B达到共同速度前A不滑离木板,木板至少多长?