半径为R，均匀带正电荷的球体在空间产生球对称的电场；场强大小沿半径分布如图所示，图中E0已知，E－r曲线下O－R部分的面积等于R－2R部分的面积。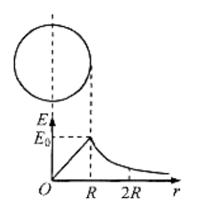
（1）写出E－r曲线下面积的单位；
（2）已知带电球在r≥R处的场强E=kQ／r2，式中k为静电力常量，该均匀带电球所带的电荷量Q为多大?
（3）求球心与球表面间的电势差△U；
（4）质量为m，电荷量为q的负电荷在球面处需具有多大的速度可以刚好运动到2R处?
如图所示，两根足够长、电阻不计的光滑平行金属导轨相距为L＝1m，导轨平面与水平面成θ＝30°角，上端连接阻值R＝1.5Ω的电阻；质量为m＝2kg、阻值r＝0.5Ω的金属棒ab放在两导轨上，棒与导轨垂直并保持良好接触。整个装置处于一匀强磁场中，该匀强磁场方向与导轨平面垂直，磁感应强度大小为2.0T。现由静止释放金属棒，金属棒在下滑过程中始终与框架垂直，g=10m/s2求：
（1）金属棒沿光滑平行金属导轨运行的最大速度
（2）当金属棒速度为4m/s时，金属棒的加速度是多少？
（3）若从静止释放到金属棒速度达到最大这一过程中电阻R上产生焦耳热是0.75J，则金属棒沿金属框架下滑的距离是多少？
两块水平放置的金属板间的距离为d，用导线与一个
匝线圈相连，线圈电阻为r，线圈中有竖直向上均匀变化的磁场，电阻R与金属板连接，如图所示。两板间有一个质量为m，电荷量为+q的油滴恰好处于静止状态，当地的重力加速度为g。则线圈中的磁感应强度B的变化情况和其磁通量的变化率为多少？
如图所示为一个小型旋转电枢式交流发电机的原理图，其矩形线圈的长度ab＝0.25 m，宽度bc＝0.20 m，共有n＝100匝，总电阻r＝1.0 Ω，可绕与磁场方向垂直的对称轴OO′转动．线圈处于磁感应强度B＝
T的匀强磁场中，与线圈两端相连的金属滑环上接一个额定电压为3.0 V的灯泡。当线圈以角速度7.2rad/s匀速转动时，小灯泡恰好能正常发光。求：
（1）线圈转动时产生的感应电动势的最大值
（2）小灯泡的额定功率
（3）线圈以上述角速度转动一周过程中发电机产生的电能
动量分别为5kgm/s和6kgm/s的小球A、B沿光滑平面上的同一条直线同向运动，A追上B并发生碰撞后.若已知碰撞后A的动量减小了2kgm/s，而方向不变，那么A、B质量之比的可能范围是什么？
粤公网安备 44130202000953号