回热式制冷机是一种深低温设备,制冷极限约50K.某台设备工作时,一定量的氦气(可视为理想气体)缓慢经历如图所示的四个过程:从状态A到B和C到D是等温过程,温度分别为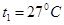 和
和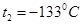 ;从状态B到C和D到A是等容过程,体积分别为V0和5V0.求状态B与D的压强之比.
;从状态B到C和D到A是等容过程,体积分别为V0和5V0.求状态B与D的压强之比.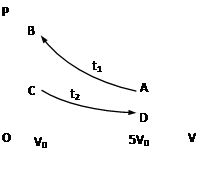
回热式制冷机是一种深低温设备,制冷极限约50K.某台设备工作时,一定量的氦气(可视为理想气体)缓慢经历如图所示的四个过程:从状态A到B和C到D是等温过程,温度分别为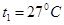 和
和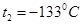 ;从状态B到C和D到A是等容过程,体积分别为V0和5V0.求状态B与D的压强之比.
;从状态B到C和D到A是等容过程,体积分别为V0和5V0.求状态B与D的压强之比.