如图所示,在同一竖直平面内,一轻质弹簧一端固定,静止斜靠在光滑斜面上,另一自由端恰好与水平线AB齐平,一长为L的轻质细线一端固定在O点,另一端系一质量为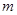
的小球,O点到AB的距离为2L.现将细线拉至水平,小球从位置C由静止释放,到达O点正下方时,细线刚好被拉断.当小球运动到A点时恰好能沿斜面方向压缩弹簧,不计碰撞时的机械能损失,弹簧的最大压缩量为
(在弹性限度内),求: 
（1）细线所能承受的最大拉力F；
（2）斜面的倾角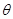
；
（3）弹簧所获得的最大弹性势能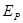
.
所含分子数量多少？这些
分子的平均间距（取两位有效数字）
，体积为
的一小块金刚石中含有多少碳原子？并估算碳原子的直径（取两位有效数字）
的油膜，试估算油分子直径的大小．相关知识点
如图所示,在同一竖直平面内,一轻质弹簧一端固定,静止斜靠在光滑斜面上,另一自由端恰好与水平线AB齐平,一长为L的轻质细线一端固定在O点,另一端系一质量为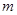的小球,O点到AB的距离为2L.现将细线拉至水平,小球从位置C由静止释放,到达O点正下方时,细线刚好被拉断.当小球运动到A点时恰好能沿斜面方向压缩弹簧,不计碰撞时的机械能损失,弹簧的最大压缩量为 (在弹性限度内),求:
（1）细线所能承受的最大拉力F；
（2）斜面的倾角；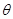
（3）弹簧所获得的最大弹性势能.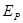
粤公网安备 44130202000953号