如图所示，倾角为θ的斜面AB是粗糙且 绝缘的，AB长为L，C为AB的中点，在 AC之间加一方向垂直斜面向上的匀强电场，与斜面垂直的虚线CD为电场的边界。现有一质量为m、电荷量为q的带正电的小物块（可视为质点），从B点开始以速度v0沿斜面向下做匀速运动，经过C点后沿斜面做匀加速运动，到达A点时的速度大小为v，试求：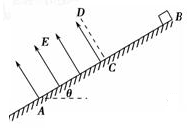
（1）小物块与斜面间的动摩擦因数μ；
（2）匀强电场场强E的大小；
（3）保持其他条件不变，使匀强电场在原区域内（AC间）顺时针转过90°，求小物块离开电场区时的动能EK大小。
如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接。现将一滑块（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点。已知A点距水平面的高度h=0.8m，B点距C点的距离L=2.0m。（滑块经过B点时没有能量损失，g=10m/s2），求：
（1）滑块在运动过程中的最大速度；
（2）滑块与水平面间的动摩擦因数μ；
（3）滑块从A点释放后，经过时间t=1.0s时速度的大小。
某课外小组经长期观测，发现靠近某行星周围有众多卫星，且相对均匀地分布于行星周围，假设所有卫星绕该行星的运动都是匀速圆周运动，通过天文观测，测得离行星最近的一颗卫星的运动半径为R1，周期为T1，已知万有引力常为G。求：
⑴行星的质量；
⑵若行星的半径为R，行星的第一宇宙速度；
⑶通过天文观测，发现离行星很远处还有一颗卫星，其运动半径为R2，周期为T2，试估算靠近行星周围众多卫星的总质量。
如图所示，半径为R，内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点c时，对管上部的压力为3mg，b通过最高点c时，对管下部的压力为0．75mg。求a,b两球落地点间的距离。
为了研究太阳演化进程，需知道目前太阳的质量M。已知地球半径
，地球质量
，日地中心距离
，地球表面处的重力加速度
，地球绕太阳一周所用的时间1年约为
，试估算目前太阳的质量M（保留一位有效数字，引力常量未知）
粤公网安备 44130202000953号