(10分）如图所示，水平放置的两块平行金属板长l =5cm，两板间距d=1cm，两板间电压为U=90V，且上板带正电，一个电子沿水平方向以速度v0=2.0×107m/s，从两板中央射入，(电子质量m=9.0×10-31kg，电子电量值q=1.6×10-19C)求：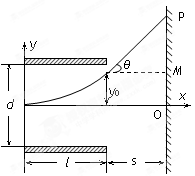
（1）电子飞出金属板时侧位移y0是多少？
（2）电子离开电场后，打在屏上的P点，若s=10cm，求OP的长．
如图所示，水平放置的平行金属板的N板接地，M板电势为＋U，两板间距离d，d比两板的尺寸小很多，在两板中间有一长为2l(2l＜d)的绝缘轻杆，可绕水平固定轴O在竖直面内无摩擦地转动，O为杆的中点．杆的两端分别连着小球A和B，它们的质量分别为2m和m，电荷量分别为＋q和－q.当杆从图示水平位置由静止开始转过90°到竖直位置时，不考虑A、B两小球间的库仑力，已知重力加速度为g，求：
(1)两小球电势能的变化；
(2)两小球的总动能．
如图所示，在水平转台上放有A、B两个小物块，它们到轴心O的距离分别为rA="0.2" m,rB="0.5" m,它们与台面间静摩擦力的最大值为其重力的0.4倍，取g="10" m/s2。
(1)当转台转动时，要使两物块都不相对台面滑动，求转台角速度的最大值；
(2)当转台转动时，要使两物块都相对台面滑动，求转台转动的角速度应满足的条件；
(3)现保持A、B两个小物块位置不变，用水平轻杆将两物块连接， 已知mA=5 mB , mB="2" kg。当转台转动角速度为某一值时，两物块恰好对台面未发生相对滑动，求此状态下轻杆对物块B的弹力。
做圆周运动，摆动到距离地面高为H=0.8m的最低点时绳子恰好断开。经测量知水平射程为S=1.6m，取g=10米每平方秒,m＝1000克,绳长为1米。求：
（1）绳子恰好断开时小球的速度；
（2）细绳能承受的最大拉力F为多少牛顿？
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍。经观测某双星系统中两颗恒星A、B围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T。已知恒星A、B之间的距离为L，A、B的质量之比2 ：1，万有引力常量为G，求：
(1) 恒星A做匀速圆周运动的轨道半径RA；
(2) 双星的总质量M 。
粤公网安备 44130202000953号