如图所示,重量为G=100 N、长为L=2m的均匀木棒放在倾斜的粗糙斜面上,斜面与水平桌面的夹角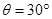 ,如图(甲)所示,至少要用35N的平行斜面的推力,才能使它从原地开始运动。木棒从原地移动以后,用10N的平行斜面的推力,就可以使木棒继续做匀速运动。求:
,如图(甲)所示,至少要用35N的平行斜面的推力,才能使它从原地开始运动。木棒从原地移动以后,用10N的平行斜面的推力,就可以使木棒继续做匀速运动。求: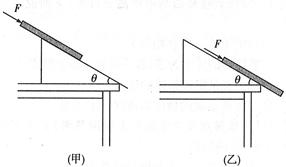
(1)木棒与桌面问的最大静摩擦力Fmax;
(2)木棒与桌面间的动摩擦因数 ;
;
(3)当平行斜面的推力使木棒匀速运动至木棒有0.6m露出斜面时,如图(乙)所示,则此时的滑动摩擦力是多少?
如图所示,重量为G=100 N、长为L=2m的均匀木棒放在倾斜的粗糙斜面上,斜面与水平桌面的夹角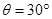 ,如图(甲)所示,至少要用35N的平行斜面的推力,才能使它从原地开始运动。木棒从原地移动以后,用10N的平行斜面的推力,就可以使木棒继续做匀速运动。求:
,如图(甲)所示,至少要用35N的平行斜面的推力,才能使它从原地开始运动。木棒从原地移动以后,用10N的平行斜面的推力,就可以使木棒继续做匀速运动。求:
(1)木棒与桌面问的最大静摩擦力Fmax;
(2)木棒与桌面间的动摩擦因数 ;
;
(3)当平行斜面的推力使木棒匀速运动至木棒有0.6m露出斜面时,如图(乙)所示,则此时的滑动摩擦力是多少?