如图所示,在绝缘水平面上,相距为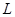 的
的 、
、 两点处分别固定着两个等量正电荷,a、b是
两点处分别固定着两个等量正电荷,a、b是 连线上两点,其中
连线上两点,其中 =
=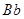 =
=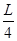 ,
,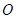 为
为 连线中点。一质量为
连线中点。一质量为 带电量为+
带电量为+ 的小滑块(可视为质点)以初动能
的小滑块(可视为质点)以初动能 从a点出发,沿
从a点出发,沿 直线向b点运动,其中小滑块第一次经过
直线向b点运动,其中小滑块第一次经过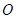 点时的动能为初动能的
点时的动能为初动能的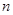 倍(
倍(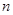 >1),到达b点时动能恰好为零,小滑块最终停在
>1),到达b点时动能恰好为零,小滑块最终停在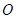 点,求
点,求
(1)小滑块与水平面间的动摩擦因数 ;
;
(2) 两点间的电势差
两点间的电势差 ;
;
(3)小滑块运动的总路程s.,
如图所示,在绝缘水平面上,相距为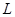 的
的 、
、 两点处分别固定着两个等量正电荷,a、b是
两点处分别固定着两个等量正电荷,a、b是 连线上两点,其中
连线上两点,其中 =
=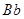 =
=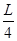 ,
,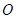 为
为 连线中点。一质量为
连线中点。一质量为 带电量为+
带电量为+ 的小滑块(可视为质点)以初动能
的小滑块(可视为质点)以初动能 从a点出发,沿
从a点出发,沿 直线向b点运动,其中小滑块第一次经过
直线向b点运动,其中小滑块第一次经过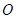 点时的动能为初动能的
点时的动能为初动能的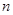 倍(
倍(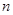 >1),到达b点时动能恰好为零,小滑块最终停在
>1),到达b点时动能恰好为零,小滑块最终停在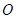 点,求
点,求
(1)小滑块与水平面间的动摩擦因数 ;
;
(2) 两点间的电势差
两点间的电势差 ;
;
(3)小滑块运动的总路程s.,