在检测某款电动车性能的实验中,质量为8×102 kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15 m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-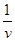 图象(图中AB、BO均为直线),假设电动车图行驶中所受的阻力恒定,求此过程中:
图象(图中AB、BO均为直线),假设电动车图行驶中所受的阻力恒定,求此过程中: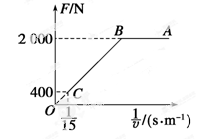
(1)电动车的额定功率;
(2)电动车由静止开始运动,经过多长时间,速度达到2 m/s?
在检测某款电动车性能的实验中,质量为8×102 kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15 m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-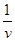 图象(图中AB、BO均为直线),假设电动车图行驶中所受的阻力恒定,求此过程中:
图象(图中AB、BO均为直线),假设电动车图行驶中所受的阻力恒定,求此过程中:
(1)电动车的额定功率;
(2)电动车由静止开始运动,经过多长时间,速度达到2 m/s?