如图甲所示,地面上有一长为l=1m,高为h=0.8m,质量M=2kg的木板,木板的右侧放置一个质量为m=1kg的木块(可视为质点),已知木板与木块之间的动摩擦因数为μ1=0.4,木板与地面之间的动摩擦因数为μ2=0.6,初始时两者均静止.现对木板施加一水平向右的拉力F,拉力F随时间的变化如图乙所示,求木块落地时距离木板左侧的水平距离△s.(取g=10m/s2)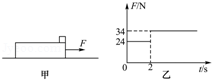
如图甲所示,地面上有一长为l=1m,高为h=0.8m,质量M=2kg的木板,木板的右侧放置一个质量为m=1kg的木块(可视为质点),已知木板与木块之间的动摩擦因数为μ1=0.4,木板与地面之间的动摩擦因数为μ2=0.6,初始时两者均静止.现对木板施加一水平向右的拉力F,拉力F随时间的变化如图乙所示,求木块落地时距离木板左侧的水平距离△s.(取g=10m/s2)